2022-2023学年贵州省三新改革联盟校高二（下）期末数学试卷

一、单选题：共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求.

• 1．已知

  z

  =

  1

  -

  i

  ，则|z|=（　　）

  A．0

  B．1

  C． 2

  D．2
  组卷：9引用：1难度：0.9

  解析

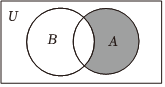• 2．设全集U={x∈N|x＜4}，A={1，2}，B={0，2}，则图中阴影部分表示的集合为（　　）

  A．∅

  B．{1}

  C．{2}

  D．{1，2}
  组卷：380引用：6难度：0.8

  解析

• 3．已知a,b,c三个数成等比，且1和4为其中的两数，则b的最小值为（　　）

  A．1

  B．-2

  C．2

  D．4
  组卷：28引用：2难度：0.7

  解析

• 4．圆C：x²+y²+4x-2y+1=0与直线l：

  x

  4

  -

  y

  3

  =0的位置关系为（　　）

  A．相切

  B．相离

  C．相交

  D．无法确定
  组卷：200引用：1难度：0.7

  解析

• 5．若一个圆锥的底面积为π，侧面展开图是一个半圆，则该圆锥的体积为（　　）

  A． 3 3 π

  B． π 2

  C． 2 2 π

  D．4π
  组卷：81引用：3难度：0.8

  解析

• 6．已知

  sinα

  =

  3

  5

  ，

  α

  ∈

  （

  π

  2

  ，

  π

  ）

  ，若

  sin

  （

  α

  +

  β

  ）

  sinβ

  =

  4

  ，则tan（α+β）=（　　）

  A． 16 7

  B． 4 7

  C． - 16 7

  D． - 4 7
  组卷：103引用：4难度：0.8

  解析

• 7．“ChatGPT”以其极高的智能化引起世界关注．深度学习是人工智能的一种具有代表性的实现方法，它是以神经网络为出发点的．在神经网络优化中，指数衰减的学习率模型为

  L

  =

  L

  0

  D

  G

  G

  0

  ，其中L表示每一轮优化时使用的学习率，L₀表示初始学习率，D表示衰减系数，G表示训练迭代轮数，G₀表示衰减速度．已知某个指数衰减的学习率模型的初始学习率为0.5，衰减速度为18，且当训练迭代轮数为18时，学习率为0.4，则学习率衰减到0.2以下（不含0.2）所需的训练迭代轮数至少为（参考数据：lg2≈0.3）（　　）

  A．75

  B．74

  C．73

  D．72
  组卷：355引用：9难度：0.5

  解析

四、解答题：共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知椭圆

  C

  ：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （

  a

  ,

  b

  ＞

  0

  ）

  的右焦点F（1，0），且经过点

  D

  （

  1

  ，

  3

  2

  ）

  ，
  （1）求椭圆C的方程；
  （2）过椭圆C左顶点A的直线与椭圆交于另一点M、与直线l：x=4交于点P，N为l与x轴的交点，求证：FP平分∠MFN．
  组卷：34引用：1难度：0.5

  解析

• 22．已知函数f（x）=ae^x-x-a.
  （1）若f（x）≥0，求a的值；
  （2）证明：当a≥1时，f（x）＞xlnx-sinx成立．
  组卷：75引用：6难度：0.4

  解析