2022-2023学年湖南省长沙实验中学高一（下）期末数学试卷

一、选择题（本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的。）

• 1．已知集合A={-1，0，1}，B={x|-1≤x＜1}，则A∩B=（　　）

  A．{0}

  B．{-1，0}

  C．{0，1}

  D．{-1，0，1}
  组卷：935引用：95难度：0.9

  解析

• 2．设a=log₂0.2，b=2^0.2，c=0.2²，则（　　）

  A．a＞b＞c

  B．c＞b＞a

  C．b＞c＞a

  D．b＞a＞c
  组卷：282引用：4难度：0.8

  解析

• 3．条件p：x²-4x-5＜0是条件q：x²+6x+5＞0的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．非充分又非必要条件
  组卷：131引用：6难度：0.9

  解析

• 4．已知空间四点A（4，1，3），B（2，3，1），C（3，7，-5），D（x,-1，3）共面，则x=（　　）

  A．4

  B．1

  C．10

  D．11
  组卷：792引用：6难度：0.9

  解析

• 5．已知某圆锥的底面半径为1，高为

  3

  ，则它的侧面积与底面积之比为（　　）

  A． 1 2

  B．1

  C．2

  D．4
  组卷：199引用：3难度：0.7

  解析

• 6．已知向量

  a

  =（2，1），

  b

  =（-1，3），则向量

  a

  在

  b

  方向上的投影向量为（　　）

  A． 1 10 b

  B． - 1 10 b

  C． 1 10 b

  D． - 1 10 b
  组卷：154引用：3难度：0.8

  解析

• 7．端午节是我国传统节日，甲，乙，丙3人端午节来徐州旅游的概率分别是：

  1

  3

  ，

  2

  5

  ，

  1

  4

  ，假定3人的行动相互之间没有影响，那么这段时间内至少有1人来徐州旅游的概率为（　　）

  A． 7 20

  B． 2 5

  C． 2 3

  D． 7 10
  组卷：541引用：5难度：0.9

  解析

四、解答题（本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）

• 21．在△ABC中，内角A，B，C所对的边分别为a,b,c,已知

  a

  +

  2

  c

  =

  bcos

  C

  +

  3

  bsin

  C

  ．
  （1）求角B；
  （2）若b=3，D为AC的中点，求线段BD长度的取值范围．
  组卷：320引用：6难度：0.7

  解析

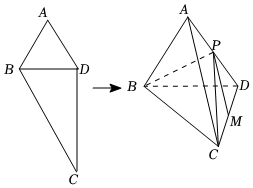• 22．已知平面四边形ABCD，AB=AD=2，∠BAD=60°，∠BCD=30°，现将△ABD沿BD边折起，使得平面ABD⊥平面BCD，此时AD⊥CD，点P为线段AD的中点．
  （1）求证：BP⊥平面ACD；
  （2）若M为CD的中点，求MP与平面BPC所成角的正弦值；
  （3）在（2）的条件下，求二面角P-BM-D的平面角的余弦值．
  组卷：631引用：9难度：0.4

  解析