2023年浙江省湖州市长兴县中考数学二模试卷

一、选择题(本题有10小题,每小题3分,共30分)下面每小题给出的四个选项中,只有一个是正确的.请选出各题中一个最符合题意的选项,并在答题卷上将相应题次中对应字母的方框涂黑,不选、多选、错选均不给分。

• 1．下列各数是无理数的是（　　）

  A．0

  B．-1

  C． 2

  D．3.14
  组卷：314引用：12难度：0.9

  解析

• 2．据中央气象台报道，某日我市最高气温是33℃，最低气温是25℃，则当天气温t（℃）的变化范围是（　　）

  A．t＞25

  B．t≤25

  C．25＜t＜33

  D．25≤t≤33
  组卷：864引用：5难度：0.9

  解析

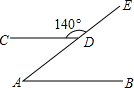• 3．如图，点A、D在射线AE上，直线AB∥CD，∠CDE=140°，那么∠A的度数为（　　）

  A．140°

  B．60°

  C．50°

  D．40°
  组卷：532引用：16难度：0.9

  解析

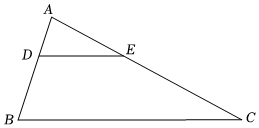• 4．如图，在△ABC中，DE∥BC，AD=2，AB=5，DE=6，则BC的长是（　　）

  A．15

  B．12

  C．9

  D．8
  组卷：136引用：1难度：0.7

  解析

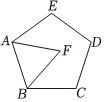• 5．如图，在正五边形内部作等边△ABF，则∠FBC的度数是（　　）

  A．30°

  B．45°

  C．48°

  D．60°
  组卷：70引用：1难度：0.7

  解析

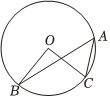• 6．如图，点A，B，C均在⊙O上，且∠BOC=90°，∠ACO=65°，则∠ABO的度数是（　　）

  A．15°

  B．20°

  C．25°

  D．30°
  组卷：115引用：1难度：0.6

  解析

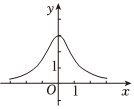• 7．运用你学习函数的经验，判断下列哪个函数的图象如图所示 （　　）

  A． y = 3 x + 1

  B．y= 3 | x + 1 |

  C． y = 3 x 2 + 1

  D． y = 3 （ x + 1 ） 2
  组卷：153引用：1难度：0.5

  解析

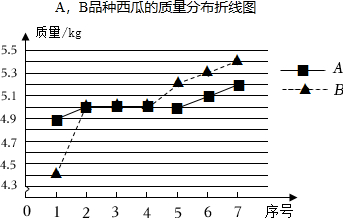
• 8．从A，B两个品种的西瓜中随机各取7个，它们的质量分布折线图如图．下列统计量中，最能反映出这两组数据之间差异的是（　　）
  

  A．平均数

  B．中位数

  C．众数

  D．方差
  组卷：584引用：8难度：0.5

  解析

三、解答题(本题有8小题,共66分,各小题都必须写出解答过程）

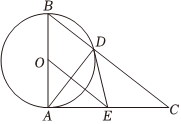• 23．如图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．
  （1）求证：ED是⊙O的切线；
  （2）若OA=3，AE=4，求BC的长；
  （3）连结OD，当∠ABC的度数为何值时，四边形AODE为正方形？并说明理由．
  组卷：114引用：1难度：0.3

  解析

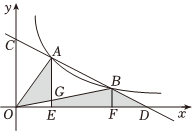• 24．如图，在平面直角坐标系xOy中，已知直线y=-

  1

  2

  x+b与坐标轴交于C，D两点，反比例函数y=

  12

  x

  （x＞0）的图象与直线CD交于A，B两点，连结AO，BO，分别过点A，B作x轴的垂线AE和BF，AE交BO于点G．
  （1）若点B的横坐标为12，求△BDF 的面积；
  （2）若阴影部分的面积为12．
  ①记△BDF 的面积为S₁，△OGE的面积为S₂，求证：_S1=2S₂；
  ②求b的值．
  组卷：121引用：1难度：0.5

  解析