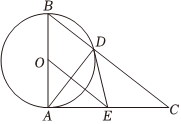
如图，已知⊙O的直径为AB，AC⊥AB于点A，BC与⊙O相交于点D，在AC上取一点E，使得ED=EA．
（1）求证：ED是⊙O的切线；
（2）若OA=3，AE=4，求BC的长；
（3）连结OD，当∠ABC的度数为何值时，四边形AODE为正方形？并说明理由．
【考点】圆的综合题．
【答案】（1）证明见解答．
（2）BC=10．
（3）当∠ABC=45°时，四边形AODE为正方形，理由见解答．
（2）BC=10．
（3）当∠ABC=45°时，四边形AODE为正方形，理由见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/6 8:0:9组卷：114引用：1难度：0.3
相似题
-
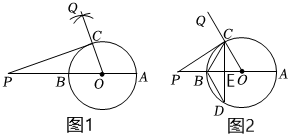1．如图1，小明在⊙O外取一点P，作直线PO分别交⊙O于B，A两点，先以点P为圆心，PO的长为半径画弧，再以点O为圆心，AB的长为半径画弧，两弧交于点Q，连接OQ，交⊙O于点C，连接PC．完成下列任务：
（1）小明得出PC为⊙O的切线的依据是 ；
（2）如图2，继续作点C关于直线AB的对称点D，连接CD，交AB于点E，连接BD．
①求证：∠PCD=2∠BDC；
②若⊙O的半径为15，BE=6，求PC的长．发布：2025/5/23 20:0:1组卷：348引用：3难度：0.3 -
2．【阅读理解】
如图1，在四边形ABCD中，AB=AD=10，BC=CD=10，∠B=90°，点M在边AD上，AM=4，点N是边BC上一动点．以MN为斜边作Rt△MNP，若点P在四边形ABCD的边AB上，则称点P是线段MN关于四边形ABCD的边AB的“直角点”．3
（1）如图1，点P是线段MN关于四边形ABCD的边AB的“直角点”，当AP=4，直接写出结果：∠BAD=；BN=．
（2）如图2，点N在运动的过程中，线段MN的中点O到BC的距离是否发生变化？若不变，请求出该距离．若变化，请说明理由．
（3）是否存在点N，使线段MN关于四边形ABCD的边AB的“直角点”恰好有两个？若存在，请直接写出BN的长度或取值范围，若不存在，请说明理由．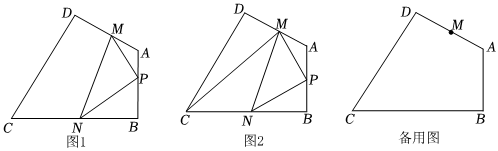
发布：2025/5/23 21:30:2组卷：109引用：1难度：0.2 -
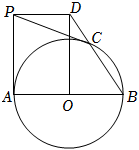3．如图，AB为⊙O直径，四边形AODP为矩形，BD交⊙O于点C，连接PC．
（1）求证：PC为⊙O的切线；
（2）若⊙O的半径是2，DO=4，则DC长为 ．发布：2025/5/23 21:0:1组卷：24引用：1难度：0.1
