2023-2024学年河南省濮阳第一高级中学高二（上）月考数学试卷（9月份）

一、选择题。本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知向量

  a

  =（1，2，1），

  b

  =（-1，0，4），则

  a

  +2

  b

  =（　　）

  A．（-1，2，9）

  B．（-1，4，5）

  C．（1，2，-7）

  D．（1，4，9）
  组卷：438引用：7难度：0.9

  解析

• 2．已知向量

  a

  =

  （

  2

  ，-

  3

  ，

  0

  ）

  ，

  b

  =

  （

  0

  ，

  3

  ，

  4

  ）

  ，则向量

  a

  在向量

  b

  方向上的投影向量为（　　）

  A． - 9 13 a

  B． 9 13 a

  C． 9 25 b

  D． - 9 25 b
  组卷：51引用：5难度：0.8

  解析

• 3．已知直线l的方向向量为

  a

  ，平面α的法向量为

  n

  ，若

  a

  =（-1，0，-1），

  n

  =（1，0，1），则直线l与平面α（　　）

  A．垂直	B．平行
  C．相交但不垂直	D．位置关系无法确定
  组卷：84引用：3难度：0.8

  解析

• 4．下列说法正确的是（　　）

  A．经过定点P（x0，y0）的直线都可以用方程y-y0=k（x-x0）表示

  B．方程x+my-2=0（m∈R）不能表示平行y轴的直线

  C．经过点P（1，1），倾斜角为θ的直线方程为y-1=tanθ（x-1）

  D．经过两点P1（x1，y1），P2（x2，y2）（x1≠x2）的直线方程为 y - y 1 = y 2 - y 1 x 2 - x 1 （ x - x 1 ）
  组卷：44引用：2难度：0.7

  解析

• 5．若

  {

  e

  1

  ，

  e

  2

  ，

  e

  3

  }

  是空间的一个基底，且向量

  {

  OA

  =

  e

  1

  +

  e

  2

  +

  e

  3

  ，

  OB

  =

  e

  1

  -

  2

  e

  2

  +

  2

  e

  3

  ，

  OC

  =

  k

  e

  1

  +

  3

  e

  2

  +

  2

  e

  3

  }

  不能构成空间的一个基底，则k=（　　）

  A． 8 3

  B． 5 2

  C． - 1 4

  D． 9 4
  组卷：74引用：5难度：0.6

  解析

• 6．已知直线kx-y-k-1=0和以M（-3，1），N（3，2）为端点的线段相交，则实数k的取值范围为（　　）

  A． - 1 2 ≤ k ≤ 3 2	B． - 2 ≤ k ≤ 2 3
  C． k ≤ - 1 2 或 k ≥ 3 2	D．k≤-2或 k ≥ 2 3
  组卷：634引用：10难度：0.7

  解析

• 7．如图，在平行六面体ABCD-A₁B₁C₁D₁中，底面是边长为1的正方形，若∠A₁AB=∠A₁AD=60°，且AA₁=2，则AC₁的长为（　　）

  A． 5

  B． 2 2

  C． 10

  D． 15
  组卷：181引用：6难度：0.8

  解析

四、解答题。本大题共6小题，满分70分，解答应写出文字说明、证明过程或演算步骤．

• 21．已知空间四边形OABC的各边及对角线的长都相等，M，N分别是OA，BC的中点，G是MN的中点，求证：
  （1）OG⊥BC；
  （2）求异面直线ON与BM所成角的余弦值．
  组卷：53引用：2难度：0.6

  解析

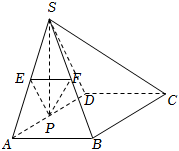• 22．如图，在四棱锥S-ABCD中，四边形ABCD是矩形，△SAD是等边三角形，平面SAD⊥平面ABCD，AB=1，P为棱AD的中点，四棱锥S-ABCD的体积为

  2

  3

  3

  ．
  （1）若E为棱SA的中点，F为棱SB的中点，求证：平面PEF∥平面SCD．
  （2）在棱SA上是否存在点M，使得平面PMB与平面SAD所成锐二面角的余弦值为

  30

  10

  ？若存在，指出点M的位置；若不存在，请说明理由．
  组卷：184引用：10难度：0.6

  解析