当前位置：试卷中心 > 试卷详情

2022-2023学年四川省成都市郫都区西川汇锦都学校九年级（上）期中数学试卷

发布：2024/9/12 12:0:9

一、选择题（本大题共8个小题，每小题4分，共32分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）

1．下列方程中，一定是关于x的一元二次方程的是（　　）
A．（x-2）（x+3）=x² B．ax²+bx+c=0
C．x²+x+2=0 D．x²+
1
x
2
=0
组卷：76引用：3难度：0.8
解析
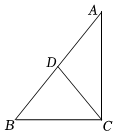2．如图，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线，若CD=2.5，AB的长为（　　）
A．2.5 B．4 C．5 D．6
组卷：422引用：4难度：0.6
解析
3．用配方法解方程x²-4x-4=0，下列变形正确的是（　　）
A．（x-2）²=2 B．（x-2）²=4 C．（x-2）²=6 D．（x-2）²=8
组卷：425引用：11难度：0.7
解析
4．若△ABC∽△DEF，且面积比为4：9，其中△ABC的周长为6cm,则△DEF的周长是（　　）
A．4cm B．9cm
C．13.5cm D．9cm或13.5cm
组卷：696引用：3难度：0.7
解析
5．在一个不透明的口袋中装有4个红球，5个白球和若干个黑球，它们除颜色外其他完全相同，通过多次摸球试验后发现，摸到白球的频率稳定在25%附近，则口袋中黑球可能有（　　）
A．10个 B．11个 C．12个 D．13个
组卷：1020引用：15难度：0.6
解析
6．关于x的一元二次方程x²+2x-a=0的一个根是1，则实数a的值为（　　）
A．0 B．1 C．2 D．3
组卷：322引用：4难度：0.7
解析
7．如图，已知直线AB∥CD∥EF，BD=2，DF=4，则
AC
AE
的值为（　　）
A．
1
3
B．
1
2
C．
2
3
D．1
组卷：1487引用：12难度：0.7
解析
8．下列四组条件中，能识别△ABC与△DEF相似的是（　　）
A．∠A=45°，∠B=55°；∠D=45°，∠F=75°
B．AB=5，BC=4，∠A=45°；DE=5，EF=4，∠D=45°
C．AB=6，BC=5，∠B=40°；DE=5，EF=6，∠E=40°
D．AB=BC，∠A=50°；DE=EF，∠E=50°
组卷：199引用：5难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

二、解答题（本大题共3个小题，共30分，解答过程写在答题卡上）

25．将矩形ABCD沿对角线BD翻折，点A落在点A′处，A′D交BC于点E，点F在CD上，连接EF，且CE=3CF，如图1．

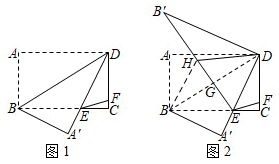
（1）试判断△BDE的形状，并说明理由；
（2）若∠DEF=45°，求tan∠CDE的值；
（3）在（2）的条件下，点G在BD上，且不与B、D两点重合，连接EG并延长到点H，使得EH=BE，连接BH、DH，将△BDH沿DH翻折，点B的对应点B′恰好落在EH的延长线上，如图2．当BH=8时，求GH的长．
组卷：896引用：2难度：0.1
解析
26．【模型建立】：（1）如图①，在Rt△ABC中，∠ACB=90°，CB=CA，直线ED经过点C，过点A作AD⊥ED于点D，过点B作BE⊥ED于点E，求证：△BEC≌△CDA；
【模型应用】：（2）如图②，已知直线l₁：y=-2x+4与x轴交于点A、与y轴交于点B，将直线l₁绕点A顺时针旋转45°至直线l₂，求直线l₂的函数表达式；
（3）如图③，平面直角坐标系内有一点B（-4，-6），过点B作BA⊥x轴于点A、BC⊥y轴于点C，点P是线段AB上的动点，点D是直线y=3x+3上的动点且在第三象限内．试探究△CPD能否成为等腰直角三角形？若能，求出点D的坐标，若不能，请说明理由．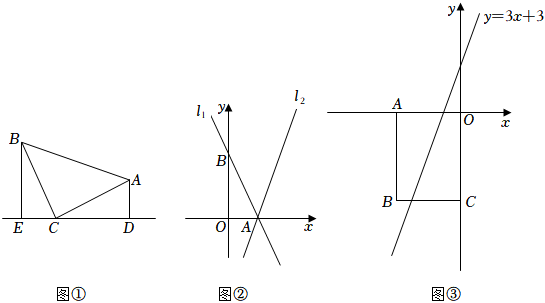
组卷：1485引用：4难度：0.3
解析