2023年贵州省铜仁三中中考数学三模试卷

一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置作答，每小题3分，共36分．

• 1．如果△+2=1，那么“△”所表示的数是（　　）

  A．-3

  B．-2

  C．-1

  D．0
  组卷：156引用：2难度：0.8

  解析

• 2．下列选项中，哪一个是不等式2x+2≥0的解（　　）

  A．-4

  B．-3

  C．-2

  D．-1
  组卷：120引用：2难度：0.6

  解析

• 3．下列运算正确的是（　　）

  A．a2+a2=a4	B．（a-b）2=a2+b2
  C．（-a+1）（-a-1）=a2-1	D．（a3）4=a7
  组卷：172引用：9难度：0.7

  解析

• 4．以下问题，不适合使用全面调查的是（　　）

  A．对新冠疫区来我市人员进行核酸检测

  B．航天飞机升空前对各零部件的安全检查

  C．了解全班学生的身高

  D．了解遵义市中小学生每周使用手机所用的时间
  组卷：44引用：3难度：0.8

  解析

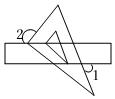• 5．如图，将含有30°的三角板的直角顶点放一块直尺的一边上，如果∠1=70°，那么∠2等于（　　）

  A．100°

  B．120°

  C．130°

  D．140°
  组卷：101引用：6难度：0.6

  解析

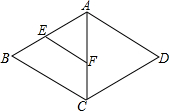• 6．如图，在菱形ABCD中，点E、F分别是AB、AC的中点，如果EF=4，那么菱形ABCD的周长是（　　）

  A．16

  B．24

  C．28

  D．32
  组卷：635引用：12难度：0.9

  解析

• 7．某超市一月份的营业额为200万元，已知第一季度的总营业额共1000万元，如果平均每月增长率为x,则由题意列方程应为（　　）

  A．200（1+x）2=1000

  B．200+200×2x=1000

  C．200+200×3x=1000

  D．200[1+（1+x）+（1+x）2]=1000
  组卷：2067引用：206难度：0.9

  解析

• 8．一次函数y=kx-1的图象经过点P，且y的值随x值的增大而增大，则点P的坐标可以为（　　）

  A．（-5，3）

  B．（1，-3）

  C．（2，2）

  D．（5，-1）
  组卷：3946引用：40难度：0.7

  解析

三、解答题：本大题有9个小题，共98分，解答应写出必要的文字说明、证明过程或演算步骤.

• 24．【提出问题】
  （1）如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等边△AMN，连接CN．求证：∠ABC=∠ACN．
  【类比探究】
  （2）如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．
  【拓展延伸】
  （3）如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连接AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连接CN．试探究∠ABC与∠ACN的数量关系，并说明理由．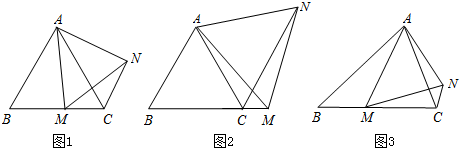
  
  组卷：6129引用：89难度：0.5

  解析

• 25．如图1，在平面直角坐标系xOy中，直线y=

  1

  2

  x-2与x轴交于点B，与y轴交于点C．抛物线y=ax²+bx+c的对称轴是直线x=

  3

  2

  且经过B、C两点，与x轴的另一交点为点A．
  
  （1）①直接写出点A的坐标；
  ②求抛物线解析式．
  （2）如图2，若点P为直线BC下方的抛物线上的一点，连接PB、PC．求△PBC的面积的最大值，并求出此时点P的坐标．
  （3）抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．
  组卷：428引用：3难度：0.1

  解析