2022-2023学年江苏省常州高级中学高一（下）质检数学试卷（5月份）

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知α，β，γ是三个不同的平面，m,n是两条不同的直线，则下列命题中正确的是（　　）

  A．若α⊥γ，β⊥γ，则α∥β	B．若m∥α，m∥β，则α∥β
  C．若m⊥α，n⊥α，则m∥n	D．若m∥α，n∥α，则m∥n
  组卷：76引用：8难度：0.6

  解析

• 2．设a是直线，α是平面，则能推出a∥α的条件是（　　）

  A．存在一条直线b,a∥b,b⊂α

  B．存在一条直线b, a ⊥ b ，b⊥α

  C．存在一个平面β，a⊂β，α∥β

  D．存在一个平面β，a⊥β，α⊥β
  组卷：24引用：6难度：0.6

  解析

• 3．已知复数

  z

  =

  i

  2023

  1

  +

  2

  i

  （i是虚数单位），则z在复平面内对应的点位于（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：64引用：4难度：0.8

  解析

• 4．在长方体ABCD-A₁B₁C₁D₁中，AB=1，BC=2，AA₁=5，则A₁C与平面ABCD所成角的正切值为（　　）

  A． 1 2

  B．2

  C． 5 5

  D． 5
  组卷：211引用：3难度：0.5

  解析

• 5．若正三棱锥的底面边长等于a,三条侧棱两两垂直，则它的侧面积为（　　）

  A． 3 4 a 2

  B． 3 4 a 2

  C． 3 2 a 2

  D．3a2
  组卷：89引用：2难度：0.7

  解析

• 6．已知0＜α＜π，且sinα+cosα=-

  1

  5

  ，则cosα-sinα=（　　）

  A．- 7 5

  B． 7 5

  C．- 37 5

  D． 37 5
  组卷：98引用：3难度：0.7

  解析

• 7．已知函数

  f

  （

  x

  ）

  =

  cos

  （

  2

  ωx

  -

  π

  6

  ）

  （

  ω

  ＞

  0

  ）

  的最小正周期为

  π

  2

  ，将f（x）的图象向左平移

  π

  6

  个单位长度，再把得到的曲线上各点的横坐标伸长到原来的2倍，得到函数g（x）的图象，则下列结论不正确的是（　　）

  A．g（0）=0

  B．g（x）的图象关于点 （ π 2 ， 0 ） 对称

  C．g（x）的图象关于 x = - π 4 对称

  D．g（x）在 [ - π 12 ， π 3 ] 上的最大值是1
  组卷：265引用：3难度：0.5

  解析

四、解答题：本题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤．

• 21．已知a,b,c分别为△ABC三个内角A，B，C的对边，且

  acos

  C

  +

  3

  asin

  C

  =

  b

  +

  c

  ．
  （1）求A；
  （2）若AD为BC边上的中线，

  cos

  B

  =

  2

  7

  7

  ，

  AD

  =

  19

  2

  ，求△ABC的面积．
  组卷：184引用：2难度：0.7

  解析

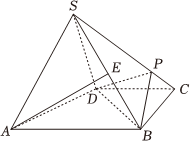• 22．如图，在四棱锥S-ABCD中，AB∥DC，AB=2DC．
  （1）已知BC⊥AB，CD=SD，平面SCD⊥平面SBC，求证：BC⊥平面SCD；
  （2）已知E，P分别是侧棱SB，SC上一点，且SP=4PC，若AE∥平面PBD，求

  SE

  EB

  的值．
  
  组卷：104引用：2难度：0.6

  解析