2020-2021学年江苏省南京市玄武区七年级（下）期末数学试卷
发布：2024/5/25 8:0:9
一、选择题（本大题共6小题，每小题2分，共12分．在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卡相应位置上）
-
1．下列各式中，计算结果为a7（ ）
组卷：68引用：2难度：0.8 -
2．若a＞3，则下列各式中，不成立的是（ ）
组卷：57引用：1难度：0.8 -
3．下列命题中，假命题是（ ）
组卷：75引用：1难度：0.7 -
4．已知
是方程组x=3y=-2的解，则a+b的值是（ ）ax+by=2bx+ay=-3组卷：472引用：7难度：0.7 -
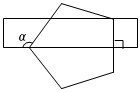5．如图，将透明直尺叠放在正五边形上，若正五边形的两个顶点在直尺的边上，且一边与直尺的一边垂直，则∠α的度数为（ ）组卷：119引用：1难度：0.8 -
6．星期天，小华与同学们一起去登山．如图，上午9点从M地出发，到达山顶后休息游玩2小时，下午4点前必须按原路返回到M地．已知从M地到A、B、C、D四个山顶的上山路程分别为7千米、8千米、9千米、10千米，上山的平均速度为3千米/时，下山的平均速度为4千米/时，则小华与同学们最远可以到达（ ）组卷：195引用：1难度：0.6
二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）
-
7．我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了0.000000022米．用科学记数法表示0.000000022为米．
组卷：383引用：11难度：0.9 -
8．命题：“两直线平行，则同旁内角互补”的逆命题为．
组卷：1972引用：50难度：0.7
三、解答题（本大题共10小题，共68分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
-
25．某新建商场设有百货、服装和家电共三个经营部．该商场共有售货员190名，计划每天的销售总额为60万元，根据经验，每1万元的销售额所需售货员人数、所得利润的情况如表格．现将商场的售货员、每天销售总额根据表格中的信息全部分配到百货、服装和家电这三个经营部．
（1）若分配到百货部每天的销售额为16万元，求分配到服装部、家电部每天的销售额分别是多少万元？经营部 每1万元销售额所需人数 每1万元销售额所得利润 百货 5名 0.3万元 服装 4名 0.5万元 家电 2名 0.2万元
（2）若要求商场每天的总利润不低于19万元，求分配到服装部每天的销售额至少为多少万元？此时，分配到三个经营部的售货员分别是多少名？组卷：262引用：1难度：0.6 -
26．规定：一条直线将三角形分割为两个图形，若其中一个新三角形与原三角形有两个角分别相等，则称这条直线为原三角形的恰巧线．例如：如图①，在△ABC中，直线DE将△ABC分割为两个图形，若新三角形ADE与原三角形ABC有∠A=∠A．∠ADE=∠B，则称直线DE为△ABC的恰巧线．
（1）如图②，已知△ABC，且∠ACB=90°，AC＞BC，则下列直线中，是△ABC的恰巧线的是 ．（填上所有正确的序号）
①△ABC的角平分线CD所在的直线；
②△ABC的AB边上的高CE所在的直线；
③△ABC的AB边上的中线CF所在的直线．
（2）在△ABC中，∠A=50°，∠B=70°，点D，E分别在AB，AC边上（不与端点重合），若直线DE是△ABC的恰巧线，则∠AED的度数为 °．
（3）如图③，在△ABC中，∠ACB=90°，CD⊥AB，垂足为D，直线BE是△ABC的恰巧线，分别交AC于点E，交CD于点F，连接DE，且∠A=∠ADE．求证：直线EF是△CDE的恰巧线．
（4）如图④，△ABC是锐角三角形，∠A＜∠B＜∠C，P是AC边上的定点．在图④中，画出所有经过点P的△ABC的恰巧线示意图，并写出每一条恰巧线须满足的两组相等的角，不必说明理由．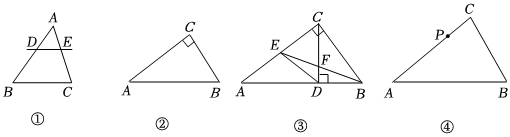
组卷：328引用：1难度：0.3
