2023年湖南师大附中高考数学摸底试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设集合A={x∈N^*|2^x＜4}，B={x∈N|-1＜x＜2}，则A∪B=（　　）

  A．{x|-1＜x＜2}

  B．{x|x＜2}

  C．{0，1}

  D．{1}
  组卷：331引用：15难度：0.7

  解析

• 2．若复数z满足|z|=|z+2i|，其中i是虚数单位，则复数z的虚部是（　　）

  A．1

  B．-1

  C．i

  D．-i
  组卷：45引用：2难度：0.8

  解析

• 3．函数f（x）=log_a|x|+1（0＜a＜1）的图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：502引用：41难度：0.9

  解析

• 4．快递公司计划在某货运枢纽附近投资配建货物分拣中心．假定每月的土地租金成本与分拣中心到货运枢纽的距离成反比，每月的货物运输成本与分拣中心到货运枢纽的距离成正比．经测算，如果在距离货运枢纽10km处配建分拣中心，则每月的土地租金成本和货物运输成本分别为2万元和8万元．要使得两项成本之和最小，分拣中心和货运枢纽的距离应设置为（　　）

  A．5km

  B．6km

  C．7km

  D．8km
  组卷：46引用：2难度：0.5

  解析

• 5．八卦是中国古老文化的深奥概念，下图示意太极八卦图．现将一副八卦简化为正八边形ABCDEFGH，设其边长为a,中心为O，则下列选项中不正确的是（　　）
  

  A． AB • AC = AB • AD	B． OA • OB + OC • OF = 0
  C． EG 和 HD 是一对相反向量	D． | AB - BC + CD + EF - FG | = a
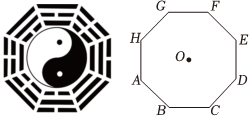  组卷：257引用：8难度：0.7

  解析

• 6．已知

  sin

  （

  π

  6

  -

  α

  ）

  =

  2

  3

  ，则

  cos

  （

  2

  α

  -

  4

  π

  3

  ）

  =（　　）

  A． - 5 9

  B． 5 9

  C． - 1 3

  D． 1 3
  组卷：570引用：4难度：0.6

  解析

• 7．已知{a_n}是公差为3的等差数列，其前n项的和为S_n，设甲：{a_n}的首项为零；乙：S₂+3是S₁+3和S₃+3的等比中项，则（　　）

  A．甲是乙的充分不必要条件

  B．甲是乙的必要不充分条件

  C．甲是乙的充要条件

  D．甲既不是乙的充分条件也不是乙的必要条件
  组卷：77引用：1难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知正项数列{a_n}满足：a₁=3，且a_n（

  a

  2

  n

  +

  1

  -1）=2（

  a

  2

  n

  -1）a_n+1，n∈N^*．
  （1）设b_n=a_n-

  1

  a

  n

  ，求数列{b_n}的通项公式；
  （2）设c_n=

  a

  2

  n

  +

  1

  a

  2

  n

  ，求数列{c_n}的前n项和T_n，并确定最小正整数n,使得T_n为整数．
  组卷：88引用：1难度：0.4

  解析

• 22．设双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =1（a＞0，b＞0）的右焦点为F，点O为坐标原点，过点F的直线l与C的右支相交于A，B两点．
  （1）当直线l与x轴垂直时，OA⊥OB，求C的离心率；
  （2）当C的焦距为2时，∠AOB恒为锐角，求C的实轴长的取值范围．
  组卷：239引用：4难度：0.3

  解析