2022-2023学年安徽省淮北市濉溪县龙华学校高二(下)期中数学试卷
发布:2024/6/27 8:0:9
一、单选题(本题共8小题,每小题5分,共40分,只有一个选项符合题目要求)
-
1.已知i为虚数单位,复数z=(3-i3)(1+ai)为纯虚数,则|z|=( )
组卷:69引用:3难度:0.9 -
2.若集合M={x|2x-x2>0,x∈R},N={y|y=2x-x2,x∈R},则M∩N=( )
组卷:104引用:3难度:0.7 -
3.设命题p:∃x∈R,使x2-9=0,则¬p是( )
组卷:56引用:2难度:0.7 -
4.已知实数x,y满足2x+y=2,则9x+2×3y的最小值为( )
组卷:389引用:3难度:0.7 -
5.已知函数
,则f(f(1))=( )f(x)=2x+1,x≤2|x-5|,x>2组卷:64引用:4难度:0.8 -
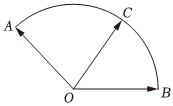 6.如图,点C是半径为1的扇形圆弧上一点,且∠AOB=ˆAB,若3π4,则x+OC=xOA+yOBy的最大值是( )2组卷:311引用:5难度:0.6
6.如图,点C是半径为1的扇形圆弧上一点,且∠AOB=ˆAB,若3π4,则x+OC=xOA+yOBy的最大值是( )2组卷:311引用:5难度:0.6 -
7.已知函数f(x)=ex-2+e2-x+2x2-8x+7,则不等式f(2x+3)>f(x+2)的解集为( )
组卷:220引用:4难度:0.6
四、解答题(本题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
-
21.在直角坐标系xOy上,椭圆
的右焦点为C:x2a2+y2b2=1(a>b>0),C的上、下顶点与F连成的三角形的面积为F(3,0).3
(1)求C的方程;
(2)已知过点F的直线l与C相交于A,B两点,问C上是否存在点Q,使得?若存出,求出l的方程.若不存在,请说明理由.OA+OB=OQ组卷:386引用:4难度:0.6 -
22.已知函数
.f(x)=ax-bx-2lnx(a>0)
(1)若a=b,讨论f(x)的单调性;
(2)当a=1,b>1,f'(x)=m有两个不同的实数根x1,x2,证明:f(x1)+f(x2)+2m>0.组卷:99引用:3难度:0.3


