当前位置：试卷中心 > 试卷详情

2022-2023学年广东省深圳实验学校高中部高二（上）第三次段考数学试卷

发布：2024/9/6 9:0:9

一、选择题

1．直线
3
x
+
y
-
2
=
0
的倾斜角是（　　）
A．
π
6
B．
π
3
C．
2
π
3
D．
5
π
6
组卷：250引用：5难度：0.9
解析
2．以椭圆
x
2
25
+
y
2
9
=1的左焦点为焦点的抛物线的标准方程是（　　）
A．y²=16x B．y²=-8x C．y²=-16x D．x²=-16y
组卷：212引用：6难度：0.9
解析
3．已知圆M与直线3x-4y=0及3x-4y+10=0都相切，圆心在直线y=-x-4上，则圆M的方程为（　　）
A．（x+3）²+（y-1）²=1 B．（x-3）²+（y+1）²=1
C．（x+3）²+（y+1）²=1 D．（x-3）²+（y-1）²=1
组卷：904引用：8难度：0.7
解析
4．记S_n为等差数列{a_n}的前n项和，有下列四个等式，甲：a₁=1；乙：S₃=9；丙：S₆=36；丁：a₄=6．如果只有一个等式不成立，则该等式为（　　）
A．甲 B．乙 C．丙 D．丁
组卷：74引用：3难度：0.8
解析
5．已知双曲线C₁过点
（
5
，
4
）
，且与双曲线C₂：
x
2
5
-
y
2
2
=
1
有相同的渐近线，则双曲线C₁的焦距为（　　）
A．7 B．14 C．
21
D．
2
21
组卷：143引用：7难度：0.7
解析
6．若圆C₁：（x-1）²+y²=1与圆C₂：（x-4）²+（y-4）²=32-m有且仅有3条公切线，则m=（　　）
A．16 B．28 C．9 D．-11
组卷：41引用：2难度：0.7
解析
7．数列{a_n}的首项a₁=2，且a_n+1=4a_n+6（n∈N^*），令b_n=log₂（a_n+2），则
b
1
+
b
2
+
…
+
b
2022
2022
等于（　　）
A．2020 B．2021 C．2022 D．2023
组卷：41引用：1难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题

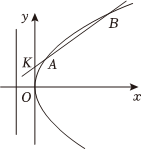21．设抛物线y²=2px（p＞0）的准线为l,A、B为抛物线上两动点，AA'⊥l于A'，定点K（0，1）使|KA|+|AA'|有最小值
2
．
（1）求抛物线的方程；
（2）当
KA
=
λ
KB
（λ∈R且λ≠1）时，是否存在一定点T满足
TA
•
TB
为定值？若存在，求出T的坐标和该定值；若不存在，请说明理由．
组卷：97引用：4难度：0.5
解析
22．已知椭圆C：
x
2
a
2
+
y
2
b
2
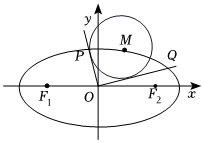=1（a＞b＞0）的离心率为
3
2
，设M（x₀，y₀）是C上的动点，以M为圆心作一个半径r=2的圆，过原点作该圆的两切线分别与椭圆C交于点P、Q，若存在圆M与两坐标轴都相切．
（1）求椭圆C的方程；
（2）若直线OP，OQ的斜率都存在且分别为k₁，k₂，求证：k₁k₂为定值；
（3）求|OP|•|OQ|的最大值．
组卷：31引用：1难度：0.5
解析