2023-2024学年山东省济宁市任城区九年级(上)期中数学试卷(五四学制)
发布:2024/10/3 20:0:1
一、选择题(本大题满分30分,每小题3分.每小题只有一个符合题意的选项,请你将正
-
1.下列各点中,在函数y=-
图象上的是( )8x组卷:1168引用:70难度:0.9 -
2.抛物线y=-3(x+2)2的对称轴是直线( )
组卷:432引用:3难度:0.5 -
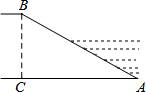 3.如图,河坝横断面迎水坡AB的坡度i=1:,坝高BC为5m,则AB的长度为( )3组卷:200引用:4难度:0.7
3.如图,河坝横断面迎水坡AB的坡度i=1:,坝高BC为5m,则AB的长度为( )3组卷:200引用:4难度:0.7 -
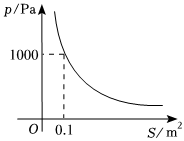 4.在压力不变的情况下,某物体承受的压强p(单位:Pa)与它的受力面积S(单位:m2)是反比例函数关系,其图象如图所示.下列说法错误的是( )组卷:501引用:5难度:0.5
4.在压力不变的情况下,某物体承受的压强p(单位:Pa)与它的受力面积S(单位:m2)是反比例函数关系,其图象如图所示.下列说法错误的是( )组卷:501引用:5难度:0.5 -
5.在△ABC中,∠A,∠B都是锐角,且sinA=
,tanB=32,则△ABC的形状是( )3组卷:1540引用:11难度:0.6 -
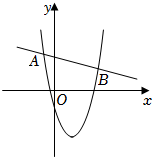 6.如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,4),B(6,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( )组卷:2700引用:14难度:0.7
6.如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,4),B(6,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( )组卷:2700引用:14难度:0.7 -
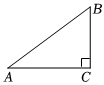 7.如图,在Rt△ABC中,,则△ABC的面积为( )∠C=90°,sinA=35,AB=10组卷:390引用:8难度:0.7
7.如图,在Rt△ABC中,,则△ABC的面积为( )∠C=90°,sinA=35,AB=10组卷:390引用:8难度:0.7 -
8.下表是小红填写的实践活动报告的部分内容:
设铁塔顶端到地面的高度FE为xm,根据以上条件,可以列出的方程为( )题目 测量铁塔顶端到地面的高度 测量目标示意图 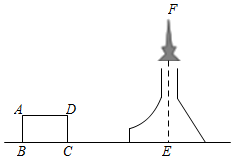
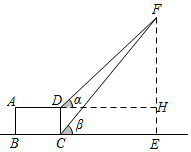
相关数据 CD=10m,α=45°,β=50° 组卷:678引用:12难度:0.7
三、解答题(本大题满分52分,解答要写出必要的文字说明或推演步骤)
-
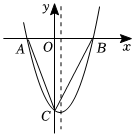 23.如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于C点,OA=2,OC=8,连接AC和BC.
23.如图,抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于C点,OA=2,OC=8,连接AC和BC.
(1)求抛物线的解析式;
(2)点D在抛物线的对称轴上,当△ACD的周长最小时,求点D的坐标.组卷:275引用:6难度:0.7 -
24.如图,抛物线y=-x2+3x+4与x轴交于点A,点B(点A在点B左侧),与y轴交于点C,连接BC,点P为线段CB上一个动点(不与点C,B重合),过点P作PQ∥y轴交抛物线于点Q.
(1)直接写出点A和点B的坐标;
(2)设P的横坐标为t,请用含t的式子表示线段PQ的长,并求出线段PQ的最大值;
(3)已知点M是抛物线对称轴上的一个点,点N是平面直角坐标系内一点,当线段PQ取得最大值时,是否存在这样的点M,N,使得四边形PBMN是菱形?若存在,求出点M的坐标;若不存在,请说明理由.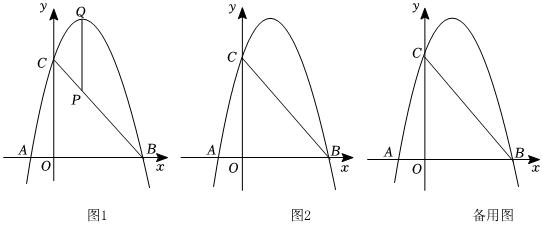 组卷:217引用:1难度:0.4
组卷:217引用:1难度:0.4


