2023-2024学年河南省郑州四中九年级（上）第一次学习比赛数学试卷

一.选择题（每小题3分，共30分）

• 1．下列关于x的方程中，一定是一元二次方程的是（　　）

  A．x-1=0

  B．x3+x=3

  C．x2+3x-5=0

  D．ax2+bx+c=0
  组卷：1382引用：31难度：0.9

  解析

• 2．下列条件中，能判定平行四边形是菱形的是（　　）

  A．对角线互相垂直	B．对角线相等
  C．对角线互相平分	D．有一个角是直角
  组卷：328引用：6难度：0.5

  解析

• 3．要检验一个四边形画框是否为矩形，可行的测量方法是（　　）

  A．测量四边形画框的两个角是否为90°

  B．测量四边形画框的对角线是否相等且互相平分

  C．测量四边形画框的一组对边是否平行且相等

  D．测量四边形画框的四边是否相等
  组卷：1645引用：8难度：0.5

  解析

• 4．已知关于x的一元二次方程x²+kx-2=0有一个根是-2，则另一个根是（　　）

  A．1

  B．-1

  C．2

  D．-2
  组卷：460引用：11难度：0.7

  解析

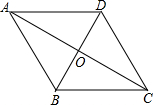• 5．如图，四边形ABCD的两条对角线相交于点O，且互相平分．添加下列条件，仍不能判定四边形ABCD为菱形的是（　　）

  A．AC⊥BD

  B．AB=AD

  C．AC=BD

  D．∠ABD=∠CBD
  组卷：3075引用：35难度：0.5

  解析

• 6．若方程x²+2x+m+1=0有两个不相等的实数根，则m的值可以是（　　）

  A．-1

  B．0

  C．1

  D． 2
  组卷：211引用：6难度：0.7

  解析

• 7．根据下表：
  

  x	-3	-2	-1	…	4	5	6
  x2-bx-5	13	5	-1	…	-1	5	13

  确定方程x²-bx-5=0的解的取值范围是（　　）

  A．-2＜x＜-1或4＜x＜5	B．-2＜x＜-1或5＜x＜6
  C．-3＜x＜-2或5＜x＜6	D．-3＜x＜-2或4＜x＜5
  组卷：825引用：22难度：0.6

  解析

三、解答题（共8小题，共75分）

• 22．阅读材料，解决问题．
  相传古希腊毕达哥拉斯学派的数学家经常在沙滩上研究数学问题．他们在沙滩上画点或用小石子来表示数，比如，他们研究过1、3、6、10…，由于这些数可以用图中所示的三角点阵表示，他们就将每个三角点阵中所有的点数和称为三角数．
  
  则第n个三角数可以用1+2+3+…+（n-2）+（n-1）+n=

  n

  （

  n

  +

  1

  ）

  2

  （n≥1且为整数）来表示．
  （1）若三角数是55，则n=

  ；
  （2）把第n个三角点阵中各行的点数依次换为2，4，6，…，2n,…，请用含n的式子表示前n行所有点数的和；
  （3）在（2）中的三角点阵中前n行的点数的和能为120吗？如果能，求出n,如果不能，请说明理由．
  组卷：122引用：4难度：0.4

  解析

• 23．综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动．
  （1）操作判断
  操作一：对折正方形纸片，使AD与BC重合，得到折痕EF，把纸片展平；
  操作二：在BE上选一点H，沿CH折叠，使点B落在EF上的点G处，得到折痕CH，把纸片展平；根据以上操作，直接写出图1中∠CHB的度数：

  ．
  （2）拓展应用
  小华在以上操作的基础上，继续探究，延长HG交AD于点M，连接CM交EF于点N（如图2）．判断△MGN的形状，并说明理由．
  （3）迁移探究
  如图3，已知正方形ABCD的边长为6cm,当点H是边AB的三等分点时，把△BCH沿CH翻折得△GCH，延长HG交AD于点M，请直接写出AM的长．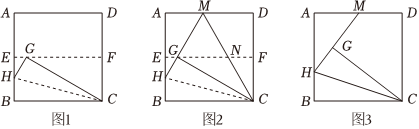
  
  组卷：830引用：3难度：0.5

  解析