2021-2022学年辽宁省朝阳市育英高中高一（下）期中数学试卷

一、单选题（每小题5分，8小题，共40分）

• 1．设全集U={n∈N|n≤10}，A={2，3，5}，B={0，3，5，9}，则（∁_UA）∩B=（　　）

  A．{2，6}

  B．{0，9}

  C．{1，9}

  D．∅
  组卷：134引用：4难度：0.9

  解析

• 2．命题“∀x≥2，x²-4x+4≥0”的否定是（　　）

  A．∀x≥2，x2-4x+4＜0	B．∃x＜2，x2-4x+4＜0
  C．∀x＜2，x2-4x+4＜0	D．∃x≥2，x2-4x+4＜0
  组卷：106引用：4难度：0.9

  解析

• 3．如果θ是第二象限角，那么

  θ

  2

  是（　　）

  A．第一或第四象限角	B．第一或第三象限角
  C．第二或第三象限角	D．第二或第四象限角
  组卷：448引用：5难度：0.9

  解析

• 4．已知命题p：-1＜x＜2，命题q：x＜-3或x≥-1，则p是q的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：27引用：2难度：0.7

  解析

• 5．已知函数f（x）=

  x + 2 ， （ x ≤ - 1 ）

  x 2 ， （ - 1 ＜ x ＜ 2 ）

  2 x , （ x ≥ 2 ）

  ，若f（x）=2，则x的值为（　　）

  A．0

  B． 2

  C．1或± 2

  D．0或1
  组卷：48引用：6难度：0.9

  解析

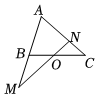• 6．如图，在△ABC中，点O是BC的中点，过点O的直线分别交直线AB，AC于不同的两点M、N，若

  AB

  =

  1

  2

  AM

  ，

  AC

  =n

  AN

  ，则n=（　　）

  A．1

  B． 3 2

  C．2

  D．3
  组卷：51引用：3难度：0.7

  解析

• 7．已知角α的顶点与坐标原点O重合，始边与x轴的非负半轴重合，终边上的一点P的坐标为（-m,3m），（m＜0），则cosα=（　　）

  A．- 3 10 10

  B．- 10 10

  C． 10 10

  D． 3 10 10
  组卷：21引用：2难度：0.7

  解析

四、解答题

• 21．已知函数

  f

  （

  x

  ）

  =

  3

  sin

  （

  2

  x

  +

  π

  6

  ）

  +

  1

  ．
  （1）求函数f（x）的最小正周期；
  （2）求函数f（x）的最值及取得最值时的x的取值集合；
  （3）求函数f（x）的单调递减区间．
  组卷：149引用：3难度：0.3

  解析

• 22．在（1）将函数f（x）图象向右平移

  π

  12

  个单位使得图象关于y轴对称； （2）函数

  y

  =

  f

  （

  x

  +

  π

  6

  ）

  是奇函数； （3）当x=

  7

  π

  12

  时，函数

  y

  =

  f

  （

  x

  -

  π

  6

  ）

  取得最大值．三个中任取一个，补充在题中的横线处，然后解得问题．
  题干：已知函数f（x）=2sin（ωx+φ），其中ω＞0，|φ|＜

  π

  2

  ，其图象相邻的对称中心之间的距离为

  π

  2

  ，___．
  （1）求函数y=f（x）的解析式及单调递增区间；
  （2）若不等式|f（x）-m|＜2在区间

  [

  π

  4

  ，

  π

  2

  ]

  上恒成立，求实数m的取值范围．
  组卷：21引用：1难度：0.6

  解析