2023-2024学年云南省大理州南涧县民族中学高二（上）见面数学试卷

一、单选题（本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，有且只有一个选项符合题目的要求）

• 1．已知全集U=R，A={x|x≤0}，B={x|x≥1}，则集合∁_U（A∪B）=（　　）

  A．{x|x≥0}

  B．{x|x≤1}

  C．{x|0≤x≤1}

  D．{x|0＜x＜1}
  组卷：1800引用：101难度：0.9

  解析

• 2．已知向量

  a

  =（m-1，1），

  b

  =（m,-2），则“m=2”是“

  a

  ⊥

  b

  ”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：825引用：12难度：0.9

  解析

• 3．函数f（x）=log₂x-

  1

  x

  的零点所在的区间为（　　）

  A．（0，1）

  B．（1，2）

  C．（2，3）

  D．（3，4）
  组卷：2239引用：30难度：0.9

  解析

• 4．某同学先后投掷一枚骰子两次，第一次向上的点数记为x,第二次向上的点数记为y,在直角坐标系xoy中，以（x,y）为坐标的点落在直线2x-y=1上的概率为（　　）

  A． 1 12

  B． 1 9

  C． 5 36

  D． 1 6
  组卷：899引用：11难度：0.9

  解析

• 5．已知m,n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题中正确的是（　　）

  A．m∥α，n∥α，则m∥n	B．m∥n,m∥α，则n∥α
  C．m⊥α，m⊥β，则α∥β	D．α⊥γ，β⊥γ，则α∥β
  组卷：1271引用：9难度：0.9

  解析

• 6．已知角α的终边在直线y=2x上，则sinα的值为（　　）

  A．±2

  B． 2 5 5

  C． ± 2 5 5

  D． ± 5 5
  组卷：390引用：3难度：0.7

  解析

• 7．在△ABC中，AD为BC边上的中线，E为AD的中点，则

  EB

  =（　　）

  A． 3 4 AB - 1 4 AC

  B． 1 4 AB - 3 4 AC

  C． 3 4 AB + 1 4 AC

  D． 1 4 AB + 3 4 AC
  组卷：17671引用：171难度：0.9

  解析

四、解答题（本题满分70分，解答应写出文字说明，证明过程和演算步骤.）

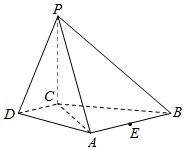• 21．如图，在四棱锥P-ABCD中，PC⊥平面ABCD，AB∥DC，DC⊥AC．
  （1）求证：DC⊥平面PAC；
  （2）求证：平面PAB⊥平面PAC；
  （3）设点E为AB的中点，在棱PB上是否存在点F，使得PA∥平面CEF？说明理由．
  组卷：7127引用：15难度：0.3

  解析

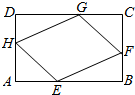• 22．如图，有一块矩形空地ABCD，要在这块空地上开辟一个内接四边形EFGH为绿地，使其四个顶点分别落在矩形的四条边上，已知AB=a（a＞2），BC=2，且AE=AH=CF=CG，设AE=x,绿地EFGH面积为y.
  （1）写出y关于x的函数解析式，并求出它的定义域；
  （2）当AE为何值时，绿地面积y最大？并求出最大值．
  组卷：131引用：7难度：0.3

  解析