当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省嘉兴市平湖市当湖高级中学高二（下）段考数学试卷（3月份）

发布：2024/7/15 8:0:9

一、单选题（每小题5分，共40分）

1．下列求导运算正确的是（　　）
A．（x^-2）′=x^-3 B．（xsinx）′=sinx+xcosx
C．（e^2x）′=e^2x D．
（
cos
π
3
）
′
=
-
sin
π
3
组卷：105引用：3难度：0.8
解析
2．设函数f（x）在x=1处的导数为2，则
lim
Δ
x
→
0
f
（
1
+
Δ
x
）
-
f
（
1
）
Δ
x
=（　　）
A．2 B．1 C．
2
3
D．6
组卷：257引用：7难度：0.8
解析
3．用数字1，2，3，4，5组成无重复数字的四位数，其中偶数的个数为（　　）
A．8 B．24 C．48 D．120
组卷：317引用：7难度：0.7
解析
4．已知函数
f
（
x
）
=
1
3
x
3
+
x
2
-
ax
,
f
′
（
1
）
=
0
，则实数a=（　　）
A．4 B．3 C．2 D．1
组卷：608引用：8难度：0.7
解析
5．函数f（x）=x-ln（2x+1）的单调递增区间是（　　）
A．
（
-
1
2
，
0
）
B．
（
-
1
2
，
1
2
）
C．
（
-
1
2
，
+
∞
）
D．
（
1
2
，
+
∞
）
组卷：632引用：4难度：0.8
解析
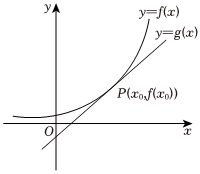6．如图，可导函数y=f（x）在点P（x₀，f（x₀））处的切线为l：y=g（x），设h（x）=f（x）-g（x），则下列说法正确的是（　　）
A．h′（x₀）=0，x=x₀是h（x）的极大值点
B．h′（x₀）=0，x=x₀是h（x）的极小值点
C．h′（x₀）=0，x=x₀不是h（x）的极值点
D．h′（x₀）≠0
组卷：39引用：2难度：0.5
解析
7．甲、乙、丙、丁、戊5名同学站成一排参加文艺汇演，若甲不站在两端，丙和丁相邻，则不同的排列方式共有（　　）
A．12种 B．24种 C．36种 D．48种
组卷：6742引用：39难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（第17题10分，18-22题每题12分，共70分）

21．已知函数f（x）=x-ln（x+1）．
（1）求f（x）的最小值；
（2）已知n∈N^*，证明：
1
+
1
2
+
1
3
+
⋯
+
1
n
＞
ln
（
n
+
1
）
；
组卷：53引用：2难度：0.6
解析
22．已知函数f（x）=lnx-ax-b（a,b∈R）．
（1）当b=0时，函数y=f（x）在
（
1
e
，
+
∞
）
上没有零点，求实数a的取值范围；
（2）当a＞0时，存在实数x₁，x₂（x₁≠x₂），使得f（x₁）=f（x₂），求证：
f
′
（
x
1
+
x
2
2
）
＜
0
．
组卷：28引用：2难度：0.5
解析