2023-2024学年吉林省通化市梅河口五中高三（上）开学数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题所给的四个选项中，只有一项是符合题目要求的.

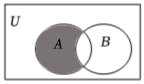• 1．设全集U=R，A={x|0＜x≤3}，B={x|x＜1}，则图中阴影部分表示的集合为（　　）

  A．{x|1≤x＜3}

  B．{x|1＜x≤3}

  C．{x|1＜x＜3}

  D．{x|1≤x≤3}
  组卷：55引用：5难度：0.7

  解析

• 2．已知

  a

  ∈

  R

  ，

  z

  =

  a

  +

  i

  1

  +

  i

  （i为虚数单位）是纯虚数，则a=（　　）

  A．-1

  B．0

  C．1

  D．2
  组卷：20引用：1难度：0.8

  解析

• 3．已知双曲线C：

  x

  2

  4

  -

  y

  2

  b

  2

  =1（b＞0）的一条渐近线方程为y=

  1

  2

  x,则C的焦距为（　　）

  A． 3

  B． 5

  C．2 3

  D．2 5
  组卷：196引用：3难度：0.9

  解析

• 4．《几何原本》是古希腊数学家欧几里得的一部不朽之作，其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥．如图，若AB，CD都是直角圆锥SO底面圆的直径，且

  ∠

  AOD

  =

  π

  3

  ，则异面直线SA与BD所成角的余弦值为（　　）

  A． 1 3

  B． 2 4

  C． 6 4

  D． 6 3
  组卷：344引用：8难度：0.7

  解析

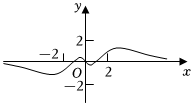• 5．已知函数f（x）的部分图象如图所示，则函数f（x）的解析式可能为（　　）

  A． f （ x ） = x - x 3 2 x	B．f（x）=e|x|•（x2-1）
  C．f（x）=x3•ln|x|	D． f （ x ） = x 3 - x e | x |
  组卷：230引用：2难度：0.8

  解析

• 6．已知集合A={x∈N|x²＜8x}，B={2，3，6}，C={2，3，7}，则B∪（∁_AC）=（　　）

  A．{2，3，4，5}	B．{2，3，4，5，6}
  C．{1，2，3，4，5，6}	D．{1，3，4，5，6，7}
  组卷：59引用：5难度：0.8

  解析

• 7．已知复数z=

  5

  3

  +

  4

  i

  ，则复数z的虚部为（　　）

  A． 4 5

  B． - 4 5

  C． 4 5 i

  D． - 4 5 i
  组卷：67引用：2难度：0.8

  解析

四、解答题（本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤）

• 21．已知函数f（x）=mx²（ln x+

  1

  2

  ）．
  （Ⅰ）若m=1，求曲线y=f（x）在（1，f（1））处的切线方程；
  （Ⅱ）当m≤1时，要使f（x）＞xlnx恒成立，求实数m的取值范围．
  组卷：127引用：3难度：0.3

  解析

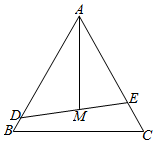• 22．某公园有一块边长为3百米的正三角形ABC空地，拟将它分割成面积相等的三个区域，用来种植三种花卉．方案是：先建造一条直道DE将△ABC分成面积之比为2：1的两部分（点D，E分别在边AB，AC上）；再取DE的中点M，建造直道AM（如图）．设AD=x,DE=y₁，AM=y₂（单位：百米）．
  （1）分别求y₁，y₂关于x的函数关系式；
  （2）试确定点D的位置，使两条直道的长度之和最小，并求出最小值．
  组卷：167引用：3难度：0.4

  解析