2022-2023学年广东省茂名一中高二（上）期中数学试卷

一、选择题（每小题5分，共8小题40分）

• 1．设y=e³，则y′等于（　　）

  A．3e2

  B．e2

  C．0

  D．e3
  组卷：43引用：8难度：0.9

  解析

• 2．设等比数列{a_n}的公比为q,若4a₂=a₁+4a₃，则q=（　　）

  A． 1 2

  B．2

  C．- 1 2

  D．-2
  组卷：1508引用：3难度：0.9

  解析

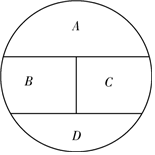• 3．如图，用4种不同的颜色对A，B，C，D四个区域涂色，要求相邻的两个区域不能用同一种颜色，则不同的涂色方法有（　　）

  A．24种

  B．48种

  C．72种

  D．96种
  组卷：668引用：7难度：0.8

  解析

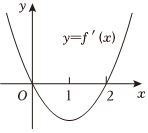• 4．设f'（x）是函数f（x）的导函数，y=f'（x）的图像如图所示，则y=f（x）的图像最有可能的是（　　）

  A．

  B．

  C．

  D．
  组卷：104引用：3难度：0.7

  解析

• 5．函数f（x）=e^|x|（2-x²）的大致图象为（　　）

  A．

  B．

  C．

  D．
  组卷：85引用：10难度：0.6

  解析

• 6．若函数f（x）=x³+x²+mx+1是R上的单调增函数，则实数m的取值范围是（　　）

  A．[ 1 3 ，+∞）

  B．（- 1 3 ，+∞）

  C．（-∞， 1 3 ]

  D．（-∞， 1 3 ）
  组卷：223引用：11难度：0.7

  解析

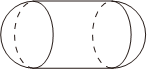• 7．如图，某几何体的形状类似胶囊，两头都是半球，中间是圆柱，其中圆柱的底面半径与半球的半径相等（半径大于1分米）．若该几何体的表面积为12π平方分米，其体积为V立方分米，则V的取值范围是（　　）

  A． （ 16 π 3 ， 4 3 π ）

  B． （ 16 π 3 ， 4 3 π ]

  C． （ 4 π ， 16 π 3 ）

  D． [ 4 π ， 16 π 3 ）
  组卷：6引用：2难度：0.6

  解析

四、解答题（共70分）

• 21．已知函数f（x）=2ax-axcosx-sinx.
  （1）当a=1时，求f（x）在[-π，π]上的值域；
  （2）当x＞0时，f（x）≥0，求实数a的取值范围．
  组卷：37引用：3难度：0.5

  解析

• 22．已知函数f（x）=

  1

  2

  x²-alnx（a∈R）
  （1）若函数f（x）在x=2处的切线方程为y=x+b,求a,b的值；
  （2）讨论方程f（x）=0解的个数，并说明理由．
  组卷：589引用：7难度：0.5

  解析