当前位置：试卷中心 > 试卷详情

2023-2024学年广东省中山一中教育集团九年级（上）第一次调研数学试卷

发布：2024/9/21 4:0:8

一.选择题（共10小题，每题3分，共30分）

1．数学世界奇妙无穷，其中曲线是微分几何的研究对象之一，下列数学曲线是中心对称图形的是（　　）
A． B． C． D．
组卷：682引用：31难度：0.8
解析
2．方程（x-3）²=4的根为（　　）
A．x₁=x₂=5 B．x₁=5，x₂=1 C．x₁=x₂=1 D．x₁=7，x₂=-1
组卷：915引用：4难度：0.7
解析
3．若方程x²+kx-2=0的一个根是-2，则k的值是（　　）
A．-1 B．1 C．0 D．-2
组卷：1213引用：17难度：0.8
解析
4．把函数y=3x²的图象向右平移1个单位，所得函数表达式为（　　）
A．y=3x²+1 B．y=3（x+1）² C．y=3x²-1 D．y=3（x-1）²
组卷：25引用：1难度：0.5
解析
5．若
（
m
-
2
）
x
m
2
-
2
-
mx
+
1
=
0
是一元二次方程，则m的值为（　　）
A．2 B．-2 C．
2
D．
-
2
组卷：1100引用：13难度：0.7
解析
6．已知点A（-2，y₁），B（-1，y₂），C（5，y₃）都在二次函数y=-x²+2x+k的图象上，则（　　）
A．y₁＜y₂＜y₃ B．y₃＜y₂＜y₁ C．y₃＜y₁＜y₂ D．y₂＜y₁＜y₃
组卷：413引用：11难度：0.6
解析
7．南宋数学家杨辉在他的著作《杨辉算法》中提出这样一个数学问题：“直田积八百六十四步，只云长阔共六十步，问长多阔几何．”意思是：一块矩形地的面积为864平方步，已知长与宽的和为60步，问长比宽多几步？设矩形的长为x步，则可列出方程为（　　）
A．x（x-60）=864 B．x（60-x）=864
C．x（x-30）=864 D．（x-30）（x-60）=864
组卷：92引用：6难度：0.7
解析
8．在中考体育训练期间，小宇对自己某次实心球训练的录像进行分析，发现实心球飞行高度y（米）与水平距离x（米）之间的关系式为y=-
1
10
x²+
3
5
x+
8
5
，由此可知小宇此次实心球训练的成绩为（　　）
A．
8
5
米 B．8米 C．10米 D．2米
组卷：1738引用：9难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

五.解答题（三）（共2小题，每小题12分，共24分）

23．定义：在平面直角坐标系xOy中，当点N在图形M的内部，或在图形M上，且点N的横坐标和纵坐标相等时，则称点N为图形M的“梦之点”．
（1）如图①，矩形ABCD的顶点坐标分别是A（-1，2），B（-1，-1），C（3，-1），D（3，2），在点M₁（1，1），M₂（2，2），M₃（3，3）中，是矩形ABCD“梦之点”的是
；
（2）如图②，已知点A，B是抛物线
y
=
-
1
2
x
2
+
x
+
9
2
上的“梦之点”，点C是抛物线的顶点．连接AC，AB，BC，求△ABC的面积；
（3）在（2）的条件下，点P为抛物线上一点，点Q为平面内一点，是否存在点P、Q，使得以AB为对角线，以A、B、P、Q为顶点的四边形是菱形？若存在，直接写出P点坐标；若不存在，请说明理由．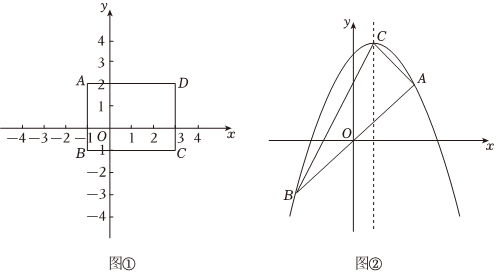
组卷：590引用：3难度：0.2
解析
24．将一副直角三角板如图1，摆放在直线MN上（直角三角板ABC和直角三角板EDC，∠EDC=90°，∠DEC=60°，∠ABC=90°，∠BAC=45°），保持三角板EDC不动，将三角板ABC绕点C以每秒5°的速度顺时针旋转，旋转时间为t秒，当AC与射线CN重合时停止旋转．
（1）如图2，当AC为∠DCE的角平分线时，求此时t的值；
（2）当AC旋转至∠DCE的内部时，求∠DCA与∠ECB的数量关系；
（3）在旋转过程中，当三角板ABC的其中一边平行于三角板EDC的某一边时，求此时t等于
（直接写出答案即可）．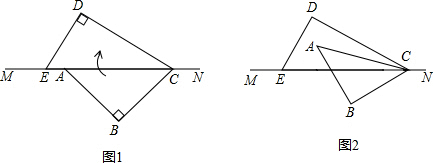
组卷：2232引用：21难度：0.4
解析