2022-2023学年浙江省金华市金东区八年级（下）期末数学试卷

一、选择题（本大题共有10小题，每小题3分，共30分，请选出一个符合题意的正确选项填涂在答题卷内，不选、多选、错选均不给分）.

• 1．下列三星堆文物图案中，既是中心对称图形又是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：138引用：6难度：0.9

  解析

• 2．若二次根式

  2

  x

  -

  1

  在实数范围内有意义，则x的取值范围是（　　）

  A．x＞ 1 2

  B．x ≥ 1 2

  C．x＞2

  D．x≥2
  组卷：369引用：8难度：0.8

  解析

• 3．在平行四边形ABCD中，∠B+∠D=110°，则∠A的度数为（　　）

  A．40°

  B．110°

  C．55°

  D．125°
  组卷：39引用：5难度：0.5

  解析

• 4．将抛物线y=x²+2向左平移3个单位长度，再向下平移4个单位长度得到的抛物线解析式为（　　）

  A．y=（x+3）2-2

  B．y=（x-3）2+6

  C．y=（x+3）2+6

  D．y=（x-3）2+2
  组卷：344引用：3难度：0.5

  解析

• 5．若x₁，x₂，x₃的方差为5，则x₁+1，x₂+1，x₃+1的方差为（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：67引用：1难度：0.7

  解析

• 6．据乘用车市场信息联席会数据显示，我国新能源车发展迅速，2023年1月至3月，新能源车月销量由33.2万辆增加到54.6万辆，设2023年1月至3月新能源车销量的月平均增长率为x,则可列方程为（　　）

  A．33.2（1+2x）=54.6

  B．33.2×2•（1+x）=54.6

  C．33.2[1+（1+x）+（1+x）2]=54.6

  D．33.2（1+x）2=54.6
  组卷：214引用：4难度：0.8

  解析

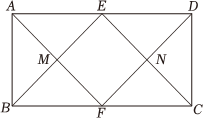• 7．如图，在矩形ABCD中，E，F分别是AD，BC的中点，连结AF，BE，CE，DF分别交于点M，N，则四边形EMFN一定是（　　）​

  A．梯形

  B．菱形

  C．矩形

  D．无法确定
  组卷：74引用：2难度：0.5

  解析

• 8．已知关于x的一元二次方程x²+4x+m=0有两个相等的实数根，则m的值是（　　）

  A．-4

  B．0

  C．4

  D．8
  组卷：460引用：6难度：0.6

  解析

三、解答题（本大题共有8小题，共66分）

• 23．根据以下素材，探索完成任务．
  

  如何设计拱桥上救生圈的悬挂方案？
  素材1	图1是一座抛物线形拱桥，以抛物线两个水平最低点连线为x轴，过抛物线离地面的最高点的铅垂线为y轴建立平面直角坐标系，如图2所示． 某时测得水面宽20m,拱顶离水面最大距离为10m,抛物线拱形最高点与x轴的距离为5m.据调查，该河段水位在此基础上再涨1m达到最高．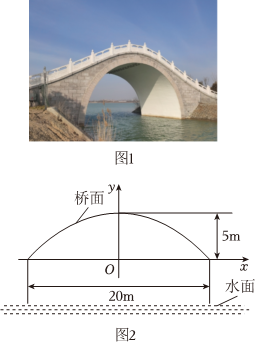
  素材2	为方便救助溺水者，拟在图1的桥拱上方栏杆处悬挂救生圈，如图3，为了方便悬挂，救生圈悬挂点距离抛物线拱面上方1m,且相邻两救生圈悬挂点的水平间距为4m.为美观，放置后救生圈关于y轴成轴对称分布．（悬挂救生圈的柱子大小忽略不计）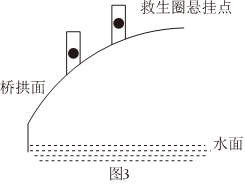
  问题解决
  任务1	确定桥拱形状	根据图2，求抛物线的函数表达式．
  任务2	拟定设计方案	求符合悬挂条件的救生圈个数，并求出最右侧一个救生圈悬挂点的坐标．
  任务3	探究救生绳长度	当水位达到最高时，上游一个落水者顺流而下到达抛物线拱形桥面的瞬间，若要确保救助者把拱桥上任何一处悬挂点的救生圈抛出都能抛到落水者身边，求救生绳至少需要多长．（救生圈大小忽略不计，结果保留整数．）
  组卷：860引用：3难度：0.5

  解析

• 24．如图，直线y=2x分别与反比例函数y₁=

  4

  x

  和y₂=

  n

  x

  （x＞0）的图象交于A，B两点，点B横坐标为2．
  （1）求n的值．
  （2）若点C为y₂=

  n

  x

  图象上一点，过点C作直线CD∥y轴，交反比例函数y₁于点D，当S_△BCD=

  1

  2

  时，求C点横坐标．
  （3）在（2）的条件下，若点E在直线AB上，请在坐标平面内找一点F，使得以C，D，E，F四点为顶点的四边形是正方形，并求出点F的坐标．
  组卷：591引用：3难度：0.2

  解析