2023-2024学年北京市昌平区融合学区(第一组)九年级(上)期中数学试卷
发布:2024/9/21 13:0:9
一、选择题(共8道小题,每小题2分,共16分)第1-8题均有四个选项,符合题意的选项只有一个
-
1.已知3a=4b(ab≠0),则下列各式正确的是( )
组卷:413引用:14难度:0.8 -
2.抛物线y=x2-2的顶点坐标是( )
组卷:307引用:9难度:0.9 -
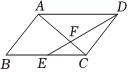 3.如图,在平行四边形ABCD中,E为BC的中点,连接DE、AC交于点F,那么的值为( )EFDF组卷:207引用:1难度:0.5
3.如图,在平行四边形ABCD中,E为BC的中点,连接DE、AC交于点F,那么的值为( )EFDF组卷:207引用:1难度:0.5 -
4.将抛物线y=x2向左平移3个单位长度,再向下平移4个单位长度,所得抛物线的表达式为( )
组卷:589引用:6难度:0.5 -
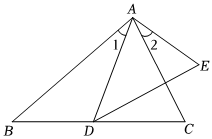 5.如图,已知∠1=∠2,那么添加下列一个条件后,不能判定△ABC∽△ADE的是( )组卷:2963引用:28难度:0.5
5.如图,已知∠1=∠2,那么添加下列一个条件后,不能判定△ABC∽△ADE的是( )组卷:2963引用:28难度:0.5 -
6.点P1(-1,y1),P2(3,y2),P3(5,y3)均在二次函数y=-(x-1)2+2的图象上,则y1,y2,y3的大小关系是( )
组卷:252引用:2难度:0.7 -
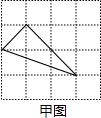 7.下列正方形方格中四个三角形中,与甲图中的三角形相似的是( )组卷:1627引用:11难度:0.9
7.下列正方形方格中四个三角形中,与甲图中的三角形相似的是( )组卷:1627引用:11难度:0.9 -
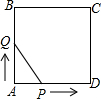 8.如图,正方形ABCD的边长为2cm,点P,点Q同时从点A出发,速度均2cm/s,点P沿A-D-C向点C运动,点Q沿A-B-C向点C运动,则△APQ的面积S(cm2)与运动时间t(s)之间函数关系的大致图象是( )组卷:1776引用:20难度:0.5
8.如图,正方形ABCD的边长为2cm,点P,点Q同时从点A出发,速度均2cm/s,点P沿A-D-C向点C运动,点Q沿A-B-C向点C运动,则△APQ的面积S(cm2)与运动时间t(s)之间函数关系的大致图象是( )组卷:1776引用:20难度:0.5
二、填空题(共8道小题,每小题2分,共16分)
-
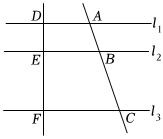 9.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,若DE=3,EF=6,AB=4,则线段BC=.组卷:118引用:2难度:0.7
9.如图,直线l1∥l2∥l3,直线AC分别交l1,l2,l3于点A,B,C,直线DF分别交l1,l2,l3于点D,E,F,若DE=3,EF=6,AB=4,则线段BC=.组卷:118引用:2难度:0.7
三、解答题(本题共12道小题,第17-22题,每小题5分,第23-26题,每小题5分,第27、28题,每小题5分,共68分)
-
27.已知等边△ABC中的边长为4,点P,M分别是边BC,AC上的一点,以点P为顶点,作∠MPN=60°,PN与直线AB交于点N.
(1)依题意补全图1;
(2)求证:BN•CM=CP•BP;
(3)如图2,若点P为BC中点,AM=2AN,求AN的长.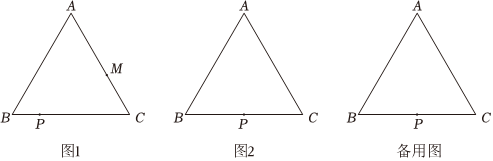 组卷:72引用:1难度:0.2
组卷:72引用:1难度:0.2 -
28.已知:如图1,抛物线的顶点为M,平行于x轴的直线与该抛物线交于点A,B(点A在点B左侧),根据对称性△AMB恒为等腰三角形,我们规定:当△AMB为直角三角形时,就称△AMB为该抛物线的“完美三角形”.
(1)①如图2,求出抛物线y=x2的“完美三角形”斜边AB的长;
②抛物线y=x2+1与y=x2的“完美三角形”的斜边长的数量关系是 ;
(2)若抛物线y=ax2+4的“完美三角形”的斜边长为4,求a的值;
(3)若抛物线y=mx2+2x+n-5的“完美三角形”斜边长为n,且y=mx2+2x+n-5的最大值为-1,求m,n的值.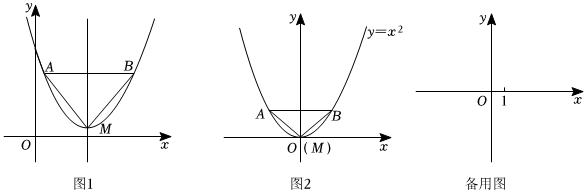 组卷:2636引用:14难度:0.5
组卷:2636引用:14难度:0.5


