2022-2023学年皖豫名校联盟高二（上）开学数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设集合A={x|x（5-x）＜0}，B={x|0＜x＜7}，则A∩B=（　　）

  A．{x|0＜x＜5}

  B．{x|5＜x＜7}

  C．{x|x＜5}

  D．{x|0＜x＜7}
  组卷：23引用：3难度：0.8

  解析

• 2．某学校有教职工x人，其中高一教师120人，高二教师120人，教学服务岗30人，其余为高三教师，现召开教职工代表大会，需要按比例用分层随机抽样的方法从中抽取28人，其中抽取高三教师10人，则x=（　　）

  A．420

  B．450

  C．480

  D．510
  组卷：3引用：1难度：0.7

  解析

• 3．已知函数f（2x+1）=log₂（x²+2x）．若f（t）=3，则t=（　　）

  A．5

  B．-7

  C．5或-7

  D．6
  组卷：3引用：2难度：0.8

  解析

• 4．已知正数a,b满足lna+lnb=ln（a+4b），则

  1

  6

  1

  a

  ×

  2

  1

  b

  =（　　）

  A．8

  B．6

  C．4

  D．2
  组卷：273引用：3难度：0.7

  解析

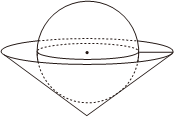• 5．如图，将一个球放入一个倒立的圆锥形容器中，圆锥的高为3，底面半径为4，且圆锥的底面恰好经过球心，则该球的表面积为（　　）

  A．16π

  B． 476 25 π

  C． 576 25 π

  D．64π
  组卷：175引用：4难度：0.5

  解析

• 6．甲、乙要从“政治”“地理”“化学”“生物”中选出2门作为自己的再选科目．已知甲同学确定选择政治，乙同学确定选择化学，他们另一门都随机选择，则他们恰有一门相同的概率为（　　）

  A． 2 3

  B． 5 9

  C． 1 2

  D． 1 3
  组卷：5引用：2难度：0.7

  解析

• 7．在△ABC中，内角A，B，C的对边分别为a,b,c,若cosA=

  3

  5

  ，B=

  π

  4

  ，且△ABC的外接圆面积为25π，则△ABC的面积为（　　）

  A．24

  B．25

  C．27

  D．28
  组卷：16引用：1难度：0.8

  解析

四、解答题：共70分.解答应写出文字说明，证明过程或演算步骤.

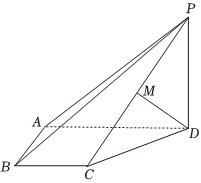• 21．如图，在四棱锥P-ABCD中，PD⊥底面ABCD，且AB=BC=

  1

  2

  AD=2，PD=2

  2

  ，∠BAD=90°，BC∥AD，M为棱PC上一点．
  （1）若PA⊥DM，证明：M为PC的中点；
  （2）求BP与平面PCD所成角的正弦值．
  组卷：6引用：2难度：0.5

  解析

• 22．已知函数f（x）=ln（

  2

  x

  2

  +a），a∈R．
  （Ⅰ）若f（x）的定义域为{x|x≠0}，值域为R，求a的值；
  （Ⅱ）若a＞0，且对任意的c∈[

  1

  2

  ，1]，当x₁，x₂∈[

  c

  ，

  c

  +

  1

  ]时，总满足|f（x₁）-f（x₂）|≤ln2，求a的取值范围．
  组卷：7引用：1难度：0.2

  解析