当前位置：试卷中心 > 试卷详情

2023-2024学年广东省深圳市罗湖外语学校九年级（上）第一次诊断数学试卷

发布：2024/9/14 5:0:10

一、选择题（本部分共10小题，每小题3分，共30分，每小题有四个选项，其中只有一个是正确的）

1．一元二次方程3x²-x=2的二次项系数、一次项系数和常数项分别是（　　）
A．3、-1、-2 B．3、-1、2 C．-3、1、-2 D．-3、-1、2
组卷：217引用：7难度：0.9
解析
2．将方程x²+2x-5=0配方后，原方程变形为（　　）
A．（x+2）²=9 B．（x-2）²=9 C．（x+1）²=6 D．（x-1）²=6
组卷：1125引用：16难度：0.6
解析
3．在一个不透明的口袋中装有4个红球，5个白球和若干个黑球，它们除颜色外其他完全相同，通过多次摸球试验后发现，摸到白球的频率稳定在25%附近，则口袋中黑球可能有（　　）
A．10个 B．11个 C．12个 D．13个
组卷：1024引用：15难度：0.6
解析
4．若关于x的一元二次方程（k-2）x²-2kx+k=6有实数根，则k的取值范围为（　　）
A．
k
≥
3
2
且k≠2 B．k≥0且k≠2 C．
k
≥
3
2
D．k≥0
组卷：1886引用：28难度：0.6
解析
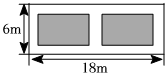5．如图，某小区有一块长为18米，宽为6米的矩形空地，计划在其中修建两块相同的矩形绿地，它们的面积之和为60平方米，两块绿地之间及周边留有宽度相等的人行通道．若设人行道的宽度为x米，则可以列出关于x的方程是（　　）
A．（18-3x）（6-2x）+60=108 B．（18-3x）（6-2x）+3x²=60
C．（18-3x）（6-2x）=60 D．108-18x-36x+3x²=60
组卷：157引用：4难度：0.8
解析
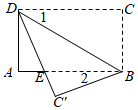6．如图，将矩形纸片ABCD沿BD折叠，得到△BC′D，C′D与AB交于点E，若∠1=40°，则∠2的度数为（　　）
A．25° B．20° C．15° D．10°
组卷：1227引用：7难度：0.6
解析
7．有一人患了流感，经过两轮传染后共有64人患了流感．设每轮传染中平均一个人传染了x个人，列出的方程是（　　）
A．x（x+1）=64 B．x（x-1）=64 C．（1+x）²=64 D．（1+2x）=64
组卷：405引用：11难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（本题共7小题，其中第16题8分，第17题5分，第18分，第20题8分，第21题9分，第22题9分，共55分）

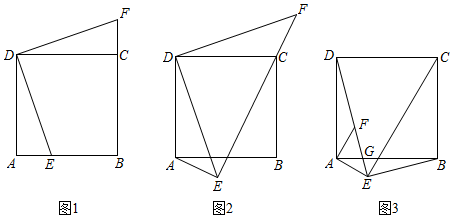
21．已知正方形ABCD，E，F为平面内两点．

【探究建模】
（1）如图1，当点E在边AB上时，DE⊥DF，且B，C，F三点共线．求证：AE=CF；
【类比应用】
（2）如图2，当点E在正方形ABCD外部时，DE⊥DF，AE⊥EF，且E，C，F三点共线．猜想并证明线段AE，CE，DE之间的数量关系；
【拓展迁移】
（3）如图3，当点E在正方形ABCD外部时，AE⊥EC，AE⊥AF，DE⊥BE，且D，F，E三点共线，DE与AB交于G点．若DF=3，AE=
2
，求CE的长．
组卷：2513引用：17难度：0.1
解析
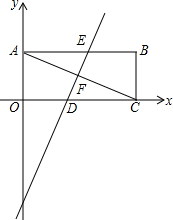22．如图，平面直角坐标系中，矩形OABC的两条邻边分别在x轴、y轴上，对角线AC=4
5
，边OA=4．
（1）求C点的坐标；
（2）把矩形OABC沿直线DE对折使点C落在点A处，直线DE与OC、AC、AB的交点分别为D，F，E，求直线DE的函数关系式；
（3）若点M是y轴上一点，点N是坐标平面内一点，问能否找到合适的点M和点N使以点M、A、D、N为顶点的四边形是菱形？如果能找到，请直接写出点M的坐标；如果找不到，请说明原因．
组卷：477引用：3难度：0.1
解析