2022-2023学年浙江省衢州市乐成寄宿中学高一（下）期中数学试卷

一、单选题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设i是虚数单位，若复数z=3+2a+（2-3a）i的实部与虚部互为相反数，则实数a=（　　）

  A．5

  B．-5

  C．3

  D．-3
  组卷：31引用：5难度：0.8

  解析

• 2．下列说法正确的是（　　）

  A．多面体至少有3个面

  B．有2个面平行，其余各面都是梯形的几何体是棱台

  C．各侧面都是正方形的四棱柱一定是正方体

  D．棱柱的侧棱相等，侧面是平行四边形
  组卷：150引用：4难度：0.8

  解析

• 3．已知α，β为锐角，

  tanα

  =

  3

  ，

  cos

  （

  α

  +

  β

  ）

  =

  -

  3

  5

  ，则tan（α-β）的值为（　　）

  A． 7 12

  B． - 7 12

  C． 7 24

  D． - 7 24
  组卷：81引用：3难度：0.7

  解析

• 4．非零向量

  a

  ，

  b

  满足：|

  a

  -

  b

  |=|

  a

  |，

  a

  •

  （

  a

  -

  b

  ）

  =

  0

  ，则

  a

  -

  b

  与

  b

  夹角的大小为（　　）

  A．135°

  B．120°

  C．60°

  D．45°
  组卷：545引用：14难度：0.7

  解析

• 5．给出的下列条件中能成为

  x

  x

  -

  3

  ≥

  0

  的充分不必要条件是（　　）

  A．x≤0或x＞3

  B．x＜-1或x＞3

  C．x≤-1或x≥3

  D．x≥0
  组卷：421引用：5难度：0.9

  解析

• 6．若

  2

  x

  +

  3

  y

  =

  1

  （

  x

  ＞

  0

  ，

  y

  ＞

  0

  ）

  ，则2x+3y的最小值为（　　）

  A．16

  B．20

  C．24

  D．25
  组卷：373引用：2难度：0.7

  解析

• 7．已知复数

  z

  =

  i

  2023

  |

  1

  +

  3

  i

  |

  -

  2

  i

  ，则8z的共轭复数为（　　）

  A．2-2i

  B．2+2i

  C． - 1 4 + 1 4 i

  D． - 1 4 - 1 4 i
  组卷：302引用：6难度：0.8

  解析

四、解答题：本大题共6小题，共70分.解答题应写出文字说明，证明过程或演算步骤.

• 21．平面内给出三个向量

  a

  =（3，2），

  b

  =（-1，2），

  c

  =（4，1），求解下列问题：
  （1）求向量

  a

  在向量

  b

  方向上的投影向量的坐标；
  （2）若向量

  a

  +

  b

  与向量

  m

  c

  +

  b

  的夹角为锐角，求实数m的取值范围；
  （3）若（

  a

  +k

  c

  ）⊥（2

  b

  -

  a

  ），求实数k的值．
  组卷：221引用：3难度：0.6

  解析

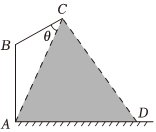• 22．在路边安装路灯，灯柱AB与地面垂直（满足∠BAD=90°），灯杆BC与灯柱AB所在平面与道路垂直，且∠ABC=120°，路灯C采用锥形灯罩，射出的光线如图中阴影部分所示，已知∠ACD=60°，路宽AD=12m.设灯柱高AB=h（m），∠ACB=θ（30°≤θ≤45°）．
  （1）当θ=30°时，求四边形ABCD的面积；
  （2）求灯柱的高h（用θ表示）；
  （3）若灯杆BC与灯柱AB所用材料相同，记此用料长度和为S，求S关于θ的函数表达式，并求出S的最小值．
  组卷：78引用：9难度：0.4

  解析