2022-2023学年重庆市缙云教育联盟高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

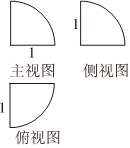• 1．如图，某几何体三视图为三个完全相同的圆心角为90°的扇形，则该几何体的表面积是（　　）

  A． π 2

  B． 3 π 4

  C． 5 π 4

  D． 7 π 4
  组卷：58引用：4难度：0.7

  解析

• 2．已知两条相交直线a,b及平面α，若a∥α，则b与α的位置关系是（　　）

  A．b⊂α

  B．b与α相交

  C．b∥α

  D．b在α外
  组卷：74引用：6难度：0.9

  解析

• 3．在△ABC中，sinA：sinB：sinC=3：5：7，则此三角形中的最大角的大小为（　　）

  A．150°

  B．135°

  C．120°

  D．90°
  组卷：169引用：3难度：0.8

  解析

• 4．设A，B，C，D是同一个半径为6的球的球面上四点，且△ABC是边长为9的正三角形，则三棱锥D-ABC体积的最大值为（　　）

  A． 81 2 4

  B． 81 3 4

  C． 243 2 4

  D． 243 3 4
  组卷：410引用：8难度：0.5

  解析

• 5．若向量

  a

  、

  b

  为两个非零向量，且

  |

  a

  |

  =

  |

  b

  |

  =

  |

  a

  -

  b

  |

  ，则向量

  a

  +

  b

  与

  a

  的夹角为（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：47引用：1难度：0.6

  解析

• 6．将一颗骰子先后抛掷2次，观察向上的点数，将第一次向上的点数记为m,第二次向上的点数记为n,曲线

  C

  ：

  x

  2

  m

  2

  +

  y

  2

  n

  2

  =

  1

  ，则曲线C的焦点在x轴上且离心率

  e

  ≤

  3

  2

  的概率等于（　　）

  A． 5 6

  B． 1 6

  C． 3 4

  D． 1 4
  组卷：39引用：1难度：0.7

  解析

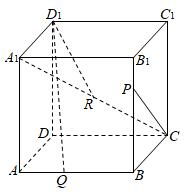• 7．已知正方体ABCD-A₁B₁C₁D₁，点P，Q，R分别是线段B₁B，AB和A₁C上的动点，观察直线CP与D₁Q，CP与D₁R给出下列结论：
  ①对于任意给定的点Q，存在点P，使得CP⊥D₁Q；
  ②对于任意给定的点P，存在点Q，使得D₁Q⊥CP；
  ③对于任意给定的点R，存在点P，使得CP⊥D₁R；
  ④对于任意给定的点P，存在点R，使得D₁R⊥CP．
  其中正确的结论是（　　）

  A．①

  B．②③

  C．①④

  D．②④
  组卷：364引用：8难度：0.5

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

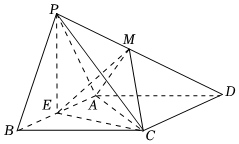• 21．如图，在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠ABC=60°，△PAB为正三角形，且侧面PAB⊥底面ABCD，E为线段AB的中点，M在线段PD上．
  （1）求证：PE⊥AC；
  （2）当点M满足

  PM

  =

  2

  MD

  时，求多面体PAECM的体积．
  组卷：62引用：2难度：0.5

  解析

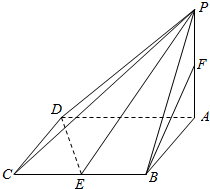• 22．在四棱锥P-ABCD中，底面ABCD是边长为2的菱形，∠BAD=60°，PA⊥面ABCD，PA=

  3

  ，E，F分别为BC，PA的中点．
  （I）求证：BF∥面PDE；
  （Ⅱ）求二面角D-PE-A的大小的正弦值；
  （Ⅲ）求点C到面PDE的距离．
  组卷：119引用：5难度：0.3

  解析