2022-2023学年贵州省遵义市高二（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分在每个小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知集合A={x|x=2k+1，k∈N}，B={x|-1≤x≤3}，则A∩B=（　　）

  A．{-1，3}

  B．{1，2，3}

  C．{1，3}

  D．{-1，0，1，2，3}
  组卷：79引用：7难度：0.8

  解析

• 2．2023年4月，国内鲜菜、食用油、粮食、禽肉、鲜果、鸡蛋、猪肉价格同比（与去年同期相比）的变化情况如图所示，则下列说法正确的是（　　）
  

  A．食用油、粮食、禽肉、鲜果、鸡蛋、猪肉这6种食品中，食用油价格同比涨幅最小

  B．猪肉价格同比涨幅超过禽肉价格同比涨幅的5倍

  C．去年4月鲜菜价格要比今年4月高

  D．这7种食品价格同比涨幅的平均值超过10%
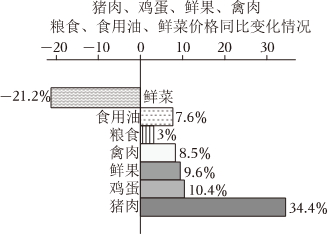  组卷：9引用：2难度：0.7

  解析

• 3．S_n为等差数列{a_n}的前n项和，a₂+a₈=6，则S₉=（　　）

  A． 27 2

  B．27

  C．54

  D．108
  组卷：107引用：23难度：0.9

  解析

• 4．下列求导运算正确的是（　　）

  A．（x3+cosx）′=3x2+sinx	B．（2x）′=2x
  C． [ ln （ 2 x + 1 ） ] ′ = 1 2 x + 1	D． （ e x x 2 ） ′ = （ x - 2 ） e x x 3
  组卷：130引用：3难度：0.8

  解析

• 5．某中学举办田径运动会，某班甲、乙等4名学生代表班级参加学校4×100米接力赛，其中甲只能跑第1棒或第2棒，乙只能跑第2棒或第4棒，那么不同棒次安排方案总数为（　　）

  A．12

  B．10

  C．8

  D．6
  组卷：28引用：3难度：0.7

  解析

• 6．将1，5，12，22等称为五边形数，如图所示，把所有的五边形数按从小到大的顺序排列，就能构成一个数列{a_n}，则该数列的第6项a₆=（　　）
  

  A．49

  B．50

  C．51

  D．52
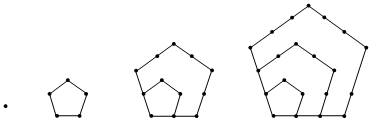  组卷：3引用：2难度：0.8

  解析

• 7．已知

  a

  =

  ln

  3

  9

  ，

  b

  =

  1

  e

  2

  ，

  c

  =

  ln

  4

  16

  ，则a,b,c的大小关系是（　　）

  A．a＞b＞c

  B．b＞a＞c

  C．b＞c＞a

  D．c＞b＞a
  组卷：23引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．甲、乙两人下象棋比赛，规则如下：由抽签确定第1局先下棋的人选，第1局先下棋的人是甲、乙的概率各为0.5，赢得本局的人下一局先下棋．若甲先下棋，则甲本局获胜的概率为0.6，若乙先下棋，则甲本局获胜的概率为0.5，每局比赛无平局且每局比赛的胜负结果相互独立
  （1）求第2局甲先下棋的概率；
  （2）若比赛采用5局3胜制，且第一局甲先下棋，记ξ为比赛结束时进行的局数，求ξ的分布列和数学期望．
  组卷：9引用：2难度：0.5

  解析

• 22．已知函数f（x）=e^x，g（x）=2-sinx-cosx.
  （1）求证：当x∈（0，+∞），x＞sinx；
  （2）若x∈（0，+∞），f（x）＞g（x）+ax恒成立，求实数a的取值范围．
  组卷：18引用：2难度：0.3

  解析