2022-2023学年浙江省湖州市高一（下）期末数学试卷

一、单选题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设集合A={x|-1＜x＜2}，集合B={x|x²-4x+3＜0}，则A∪B=（　　）

  A．{x|-1＜x＜3}

  B．{x|-1＜x＜1}

  C．{x|1＜x＜2}

  D．{x|2＜x＜3}
  组卷：319引用：4难度：0.9

  解析

• 2．若角α的终边经过点P（-1，2），则sinα等于（　　）

  A．- 5 5

  B． 2 5 5

  C． 5 5

  D．- 2 5 5
  组卷：236引用：8难度：0.9

  解析

• 3．复数z满足i²⁰²³（2+z）=2-i,则

  z

  =（　　）

  A．-1+2i

  B．1+2i

  C．-1-2i

  D．1-2i
  组卷：282引用：10难度：0.7

  解析

• 4．在空间中，l,m是不重合的直线，α，β是不重合的平面，则下列说法正确的是（　　）

  A．若l⊂α，m⊂β，α∥β，则l∥m

  B．若l∥m,m⊂β，则l∥β

  C．若α⊥β，α∩β=m,l⊥m,则l⊥β

  D．若l⊥α，l∥m,α∥β，则m⊥β
  组卷：263引用：11难度：0.7

  解析

• 5．阿基米德是伟大的古希腊数学家，他和高斯、牛顿并列为世界三大数学家，他一生最为满意的一个数学发现就是“圆柱容球”定理，即圆柱容器里放了一个球，该球顶天立地，四周碰边（即球与圆柱形容器的底面和侧面都相切），球的体积是圆柱体积的三分之二，球的表面积也是圆柱表面积的三分之二．今有一“圆柱容球”模型，其圆柱表面积为36π，则该模型中圆柱的体积与球的体积之和为（　　）

  A． 8 6 π

  B． 12 6 π

  C． 20 6 π

  D． 48 6 π
  组卷：66引用：3难度：0.6

  解析

• 6．已知向量

  a

  ，

  b

  满足

  a

  •

  b

  =

  5

  ，且

  b

  =

  （

  3

  ，-

  4

  ）

  ，则

  a

  在

  b

  上的投影向量为（　　）

  A． （ 3 5 ，- 4 5 ）

  B． （ - 3 5 ， 4 5 ）

  C．（3，-4）

  D．（-3，4）
  组卷：123引用：2难度：0.7

  解析

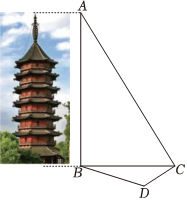• 7．“忽登最高塔，眼界穷大千．卞峰照城郭，震泽浮云天．”这是苏东坡笔下的湖城三绝之一“塔里塔”飞英塔．某学生为测量其高度，在远处选取了与该建筑物的底端B在同一水平面内的两个测量基点C与D，现测得∠BCD=45°，∠BDC=105°，CD=18米，在点C处测得飞英塔顶端A的仰角∠ACB=58°，则飞英塔的高度约是（　　）（参考数据：

  2

  ≈

  1

  .

  4

  ，

  6

  ≈

  2

  .

  4

  ，tan58°≈1.6）

  A．45米

  B．50米

  C．55米

  D．60米
  组卷：101引用：4难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

• 21．已知面积为

  2

  3

  的菱形ABCD如图①所示，其中AC=2，E是线段AD的中点．现将△DAC沿AC折起，使得点D到达点S的位置．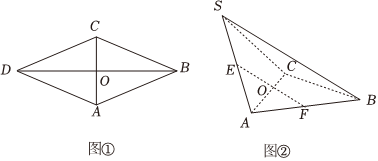
  
  （1）若二面角S-AC-B的平面角大小为

  2

  π

  3

  ，求三棱锥S-ABC的体积；
  （2）若二面角S-AC-B的平面角

  α

  ∈

  [

  π

  3

  ，

  2

  π

  3

  ]

  ，点F在三棱锥的表面运动，且始终保持EF⊥AC，求点F的轨迹长度的取值范围．
  组卷：115引用：3难度：0.5

  解析

• 22．如图，在Rt△ABC中，AB⊥AC，2AC=3AB=6，D，E，F分别在线段AC，AB，BC上，满足CD=2DA且DE⊥DF，记∠AED=α．
  （1）用含α的代数式表示sin∠DFC；
  （2）求△DEF面积的最小值．
  组卷：79引用：1难度：0.6

  解析