2021-2022学年四川省成都市新都一中高一(下)期末数学模拟试卷(4)
发布:2024/8/7 8:0:9
一、单选题
-
1.在四面体P-ABC中,E是PA的中点,F是BC的中点,设
,则PA=a,PB=b,PC=c=( )EF组卷:550引用:4难度:0.8 -
2.函数f(x)=Asin(ωx+φ)(ω>0)的图象按以下次序变换:①每个点的横坐标变为原来的2倍;②图象向右平移
个单位长度;③每个点的纵坐标变为原来的3倍.得到y=sinx的图象,则f(x)=( )π6组卷:129引用:3难度:0.8 -
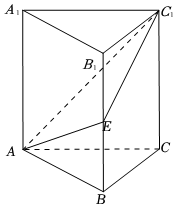 3.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2,E为BB1上一点,平面AEC1分三棱柱为上下体积相等的两部分,则AE与B1C1所成角的余弦值为( )组卷:63引用:7难度:0.6
3.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=2,E为BB1上一点,平面AEC1分三棱柱为上下体积相等的两部分,则AE与B1C1所成角的余弦值为( )组卷:63引用:7难度:0.6 -
4.已知
,a=2,b=7-3,则a,b,c的大小关系为( )c=6-2组卷:913引用:18难度:0.9 -
5.函数f(x)=sin(
-x)的单调递增区间为( )π3组卷:385引用:6难度:0.7 -
6.已知数列{an}满足a1=1,nan+1=(n+1)an+1,令
,若对于任意n∈N*,不等式bn=ann恒成立,则实数t的取值范围为( )bn+1<4-2t组卷:187引用:2难度:0.5 -
7.已知点A、B分别在二面角α-l-β的两个面α、β上,AC⊥l,BD⊥l,C、D为垂足,AC=BD=CD,若AB与l成60°角,则二面角α-l-β为( )
组卷:252引用:6难度:0.5
三、解答题
-
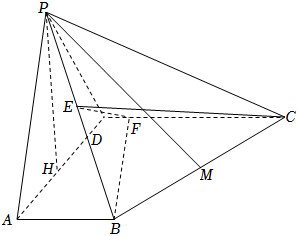 21.如图所示,在四棱锥P-ABCD中,AB∥CD,E是线段PB的中点,F是线段DC上的点,且.DF=12AB
21.如图所示,在四棱锥P-ABCD中,AB∥CD,E是线段PB的中点,F是线段DC上的点,且.DF=12AB
(1)证明:EF∥平面PAD;
(2)若AB⊥平面PAD,PD=AD,PH⊥AD,且PH∩AD=H.记直线PB与平面ABCD所成角为α,直线PB与平面PAD所成角为β,比较cosα与sinβ的大小,并说明理由.组卷:36引用:5难度:0.4 -
22.在△ABC中,角A,B,C所对的边长分别为a,b,c(b=2k,k∈N*),函数f(x)=20cos2x+3acosx-5在区间(0,bπ)上有9个零点.
(1)求a,b的值;
(2)若,求c的取值范围.cosB≤18组卷:19引用:2难度:0.5


