2023-2024学年吉林省长春市朝阳区长春外国语学校高二（上）期中数学试卷

一、单选题（本题共8小题，每题5分，共40分。在每小题列出的选项中，选出符合题目的一项）

• 1．已知圆的方程是（x-1）²+（y-3）²=4，其圆心和半径分别是（　　）

  A．（-1，-3），2

  B．（-1，-3），4

  C．（1，3），2

  D．（1，3），4
  组卷：157引用：6难度：0.7

  解析

• 2．过直线x+y-3=0和2x-y+6=0的交点，且与直线2x+y-3=0垂直的直线方程是（　　）

  A．4x+2y-9=0

  B．4x-2y+9=0

  C．x+2y-9=0

  D．x-2y+9=0
  组卷：189引用：9难度：0.7

  解析

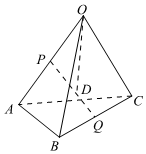• 3．如图，在三棱锥O-ABC中，点P，Q分别是OA，BC的中点，点D为线段PQ上一点，且

  PD

  =

  2

  DQ

  ，若记

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，则

  OD

  =（　　）

  A． 1 6 a + 1 3 b + 1 3 c	B． 1 3 a + 1 3 b + 1 3 c
  C． 1 3 a + 1 6 b + 1 3 c	D． 1 3 a + 1 3 b + 1 6 c
  组卷：250引用：15难度：0.7

  解析

• 4．过点P（2，4）引圆（x-1）²+（y-1）²=1的切线，则切线的方程为（　　）

  A．x=-2或4x+3y-4=0	B．4x-3y+4=0
  C．x=2或4x-3y+4=0	D．4x+3y-4=0
  组卷：181引用：1难度：0.7

  解析

• 5．唐代诗人李顾的诗《古从军行》开头两句说：“白日登山望烽火，黄昏饮马傍交河．”诗中隐含着一个有趣的数学问题——“将军饮马”问题，即将军在观望烽火之后从山脚下某处出发，先到河边饮马后再回到军营，怎样走才能使总路程最短？在平面直角坐标系中，设军营所在位置为B（3，4），若将军从点A（-2，0）处出发，河岸线所在直线方程为y=x,则“将军饮马”的最短总路程为（　　）

  A．5

  B． 3 5

  C．45

  D． 5 3
  组卷：86引用：5难度：0.8

  解析

• 6．如图，已知正四面体ABCD中，

  AE

  =

  1

  2

  AB

  ，

  CF

  =

  1

  2

  CD

  ，则异面直线DE和BF所成角的余弦值等于（　　）

  A． 2 3

  B． 3 3

  C． 6 3

  D． 3 5 10
  组卷：166引用：5难度：0.5

  解析

• 7．阿波罗尼斯（约公元前262～190年）证明过这样的命题：平面内到两定点距离之比为常数k（k＞0，k≠1）的点的轨迹是圆．后人将这个圆称为阿氏圆．若平面内两定点A，B间的距离为2，动点P与A，B的距离之比为

  2

  2

  ，当P，A，B不共线时，△PAB的面积的最大值是（　　）

  A． 2 2

  B． 2

  C． 2 2 3

  D． 2 3
  组卷：98引用：5难度：0.5

  解析

四、解答题（本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤）

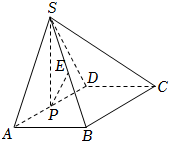• 21．如图，在四棱锥S-ABCD中，四边形ABCD是矩形，△SAD是正三角形，且平面SAD⊥平面ABCD，AB=1，P为棱AD的中点，四棱锥S-ABCD的体积为

  2

  3

  3

  ．
  （1）若E为棱SB的中点，求证：PE∥平面SCD；
  （2）在棱SA上是否存在点M，使得平面PMB与平面SAD所成锐二面角的余弦值为

  2

  3

  5

  ？若存在，指出点M的位置并给以证明；若不存在，请说明理由．
  组卷：290引用：24难度：0.5

  解析

• 22．已知两个定点M（1，0）和N（2，0），动点P满足

  |

  PN

  |

  =

  2

  |

  PM

  |

  ．
  （1）求动点P的轨迹C的方程；
  （2）若A，B为（1）中轨迹C上两个不同的点，O为坐标原点．设直线OA，OB，AB的斜率分别为k₁，k₂，k.当k₁k₂=3时，求k的取值范围．
  组卷：182引用：4难度：0.3

  解析