2023-2024学年吉林省长春外国语学校高二（上）月考数学试卷（9月份）

一、单选题（本题共8小题，每题5分，共40分。在每小题列出的选项中，选出符合题目的一项）

• 1．直线

  x

  =

  -

  tan

  π

  4

  的倾斜角是（　　）

  A．0

  B． π 4

  C． π 2

  D． 3 π 4
  组卷：428引用：4难度：0.9

  解析

• 2．在空间直角坐标系O-xyz中，点（3，1，-2）关于xOz平面的对称点的坐标为（　　）

  A．（-3，1，2）

  B．（-3，-1，2）

  C．（-2，1，3）

  D．（3，-1，-2）
  组卷：79引用：5难度：0.8

  解析

• 3．两平面α、β的法向量分别为

  u

  =（3，-1，z），

  v

  =（-2，-y,1），若α⊥β，则y+z的值是（　　）

  A．-3

  B．6

  C．-6

  D．-12
  组卷：174引用：11难度：0.7

  解析

• 4．已知空间中三角形ABC的三个顶点的坐标分别为A（2，1，1），B（0，3，2），C（0，1，0），则BC边上的中线的长度为（　　）

  A． 6

  B． 3

  C． 5

  D．2
  组卷：208引用：3难度：0.8

  解析

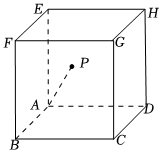• 5．如图，ABCD-EFGH是棱长为1的正方体，若P在正方体内部且满足

  AP

  =

  3

  5

  AB

  +

  1

  2

  AD

  +

  2

  3

  AE

  ，则P到直线AB的距离为（　　）

  A． 3 4

  B． 4 5

  C． 5 6

  D． 3 5
  组卷：437引用：9难度：0.5

  解析

• 6．已知A（-1，2），B（4，7），若过点C（2，0）的直线与线段AB相交，则该直线斜率的取值范围是（　　）

  A．[- 2 3 ， 7 2 ]	B．（-∞，- 2 3 ]∪[ 7 2 ，+∞）
  C．（- 3 7 ， 2 7 ）	D．（-∞，- 2 3 ）∪（ 7 2 ，+∞）
  组卷：282引用：7难度：0.8

  解析

• 7．已知MN是棱长为4的正方体内切球的一条直径，点P在正方体表面上运动，则

  PM

  •

  PN

  的取值范围为（　　）

  A．[1，4]

  B．[0，12]

  C．[0，8]

  D．[1，6]
  组卷：83引用：3难度：0.5

  解析

四、解答题（本题共5小题，共70分。解答应写出文字说明，证明过程或演算步骤）

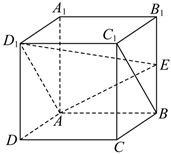• 20．如图，在棱长为2的正方体ABCD-A₁B₁C₁D₁中，E为BB₁的中点．
  （1）求证：BC₁∥平面AD₁E；
  （2）求点C到平面AD₁E的距离．
  组卷：36引用：4难度：0.5

  解析

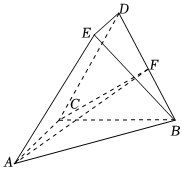• 21．如图，在五面体ABCDE中，平面BCD⊥平面ABC，AC⊥BC，ED∥AC，且AC=BC=2ED=2，

  DC

  =

  DB

  =

  3

  ．
  （1）求证：平面ABE⊥平面ABC．
  （2）线段BD上是否存在一点F，使得平面ACF与平面ABE的夹角的余弦值等于

  11

  11

  ？若存在，求

  DF

  FB

  的值；若不存在，请说明理由．
  组卷：50引用：2难度：0.4

  解析