2021-2022学年辽宁省大连二十四中高二（上）第二次统练数学试卷

一．单选题（共8小题）

• 1．已知

  a

  =

  （

  2

  ，-

  1

  ，

  3

  ）

  ，

  b

  =

  （

  -

  1

  ，

  4

  ，-

  2

  ）

  ，

  c

  =

  （

  1

  ，

  3

  ，

  λ

  ）

  ，若

  a

  ，

  b

  ，

  c

  三向量不能构成空间的一个基底，则实数λ的值为（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：21引用：1难度：0.8

  解析

• 2．直线l经过A（2，1），B（1，m²）（m∈R）两点，那么直线l的倾斜角α的取值范围是（　　）

  A．[ π 4 ， π 2 ）	B． [ 0 ， π 4 ] ∪ （ π 2 ， π ）
  C． [ 0 ， π 4 ]	D． [ π 4 ， π 2 ） ∪ （ π 2 ， π ）
  组卷：202引用：4难度：0.7

  解析

• 3．直线l：（m+1）x+（1-m）y-4m-2=0被圆C：（x-2）²+（y+3）²=9所截得的弦中，最短弦所在的直线的方程是（　　）

  A．2x+y-5=0

  B．x+2y-1=0

  C．2x-y-7=0

  D．x-2y-5=0
  组卷：26引用：4难度：0.6

  解析

• 4．在棱长为2的正四面体ABCD中，点M满足

  AM

  =x

  AB

  +y

  AC

  -（x+y-1）

  AD

  ，点N满足

  BN

  =λ

  BA

  +（1-λ）

  BC

  ，当AM、BN最短时，

  AM

  •

  MN

  =（　　）

  A．- 4 3

  B． 4 3

  C．- 1 3

  D． 1 3
  组卷：359引用：5难度：0.5

  解析

• 5．已知圆C₁：（x-1）²+（y+1）²=1，圆C₂：（x-4）²+（y-5）²=9．点M、N分别是圆C₁、圆C₂上的动点，P为x轴上的动点，则|PN|-|PM|的最大值是（　　）

  A．2 5 +4

  B．9

  C．7

  D．2 5 +2
  组卷：1219引用：20难度：0.7

  解析

• 6．平行四边形ABCD的一条对角线固定在A（3，-1），C（2，-3）两点，D点在直线3x-y+1=0上移动，则B点轨迹的方程为（　　）

  A．3x-y-20=0（x≠13）	B．3x-y-10=0（x≠13）
  C．3x-y-9=0（x≠-8）	D．3x-y-12=0（x≠-8）
  组卷：55引用：2难度：0.6

  解析

• 7．在平面直角坐标系xOy中，给定两点M（1，2），N（3，4），点P在x轴的正半轴上移动，当∠MPN取最大值时，点P的横坐标为（　　）

  A． 5 2

  B． 5 3

  C．3

  D． 10 3
  组卷：120引用：2难度：0.5

  解析

四．解答题（共6小题）

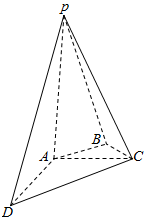• 21．如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AC⊥AD，AB⊥BC，∠BAC=45°，PA=AD=2，AC=1．
  （1）证明：PC⊥AD；
  （2）求平面PAC与平面PCD夹角的正弦值；
  （3）设E为棱PA上的点，满足异面直线BE与CD所成的角为30°，求AE的长．
  组卷：151引用：3难度：0.5

  解析

• 22．已知过点A（-1，0）的动直线l与圆C：x²+（y-3）²=4相交于P、Q两点，M是PQ中点，l与直线m：x+3y+6=0相交于N．
  （1）当PQ=2

  3

  时，求直线l的方程；
  （2）探索

  AM

  •

  AN

  是否为定值，若是，请求出其值；若不是，请说明理由．
  组卷：54引用：3难度：0.5

  解析