2023-2024学年福建省福州二中高二（上）第一次月考数学试卷

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目求的．

• 1．已知a,b∈R，a-2i=（b-i）i,若z=a+bi,则

  z

  的虚部是（　　）

  A．2

  B．1

  C．-2i

  D．2i
  组卷：108引用：15难度：0.9

  解析

• 2．设命题甲：ax²+2ax+1＞0的解集是实数集R；命题乙：0＜a＜1，则命题甲是命题乙成立的（　　）

  A．充分非必要条件	B．必要非充分条件
  C．充要条件	D．既非充分又非必要条件
  组卷：93引用：36难度：0.9

  解析

• 3．已知两个向量

  a

  =

  （

  2

  ，

  m

  ,

  3

  ）

  ，

  b

  =

  （

  4

  ，-

  1

  ，

  n

  ）

  ，且

  a

  ∥

  b

  ，则mn的值为（　　）

  A．1

  B．-2

  C．-3

  D．6
  组卷：48引用：6难度：0.8

  解析

• 4．已知空间向量

  AB

  =

  （

  1

  ，

  1

  ，

  0

  ）

  ，

  |

  AC

  |

  =

  2

  ，

  〈

  AB

  ，

  AC

  〉

  =

  3

  π

  4

  ，则

  AB

  •

  BC

  =（　　）

  A．-4

  B．0

  C．4

  D． - 2 - 2
  组卷：149引用：5难度：0.5

  解析

• 5．已知

  a

  =（2，-1，3），

  b

  =（-1，4，-2），

  c

  =（4，5，λ），如果

  a

  ，

  b

  ，

  c

  三个向量不能构成空间直角坐标系上的一组基底，则实数λ为（　　）

  A．0

  B．9

  C．5

  D．3
  组卷：842引用：9难度：0.7

  解析

• 6．已知角θ的大小如图所示，则

  1

  +

  sin

  2

  θ

  cos

  2

  θ

  =（　　）
  

  A．- 5 3

  B． 5 3

  C．-4

  D．4
  组卷：116引用：7难度：0.7

  解析

• 7．给出下列命题：
  ①若

  AB

  =

  CD

  ，则必有A与C重合，B与D重合，AB与CD为同一线段；
  ②若

  a

  •

  b

  ＜

  0

  ，则

  〈

  a

  ，

  b

  〉

  是钝角；
  ③若

  a

  是直线l的方向向量，则

  λ

  a

  （

  λ

  ∈

  R

  ）

  也是l的方向向量；
  ④非零向量

  a

  ，

  b

  ，

  c

  满足

  a

  与

  b

  ，

  b

  与

  c

  ，

  c

  与

  a

  都是共面向量，则

  a

  ，

  b

  ，

  c

  必共面．
  其中错误命题的个数是（　　）

  A．1

  B．2

  C．3

  D．4
  组卷：60引用：2难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

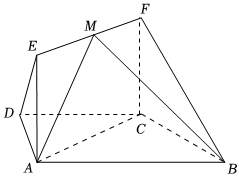• 21．如图，在等腰梯形ABCD中，AB∥CD，AD=DC=1，∠BCD=

  2

  π

  3

  ，四边形ACFE为矩形，且CF⊥平面ABCD，CF=1．
  （1）求证：EF⊥平面BCF；
  （2）在线段EF上是否存在点M，使得平面MAB与平面FCB所成锐二面角的平面角为θ，且满足

  cosθ

  =

  7

  7

  ．若不存在，请说明理由；若存在，求出EM的长度．
  组卷：162引用：5难度：0.5

  解析

• 22．如图，在平面四边形ABCD中，已知

  AB

  =

  2

  3

  ，

  ∠

  ACB

  =

  π

  3

  ．
  （1）若

  AC

  =

  2

  2

  ，求BC的长；
  （2）设∠ACD=α，∠ADC=β，若ADcosα=ACcosβ，

  α

  =

  π

  3

  ，求△ACD面积的最大值．
  组卷：216引用：3难度：0.5

  解析