2023-2024学年浙江省金华市兰溪市聚仁中学九年级（上）期中数学试卷

一、选择题

• 1．已知3a=4b（ab≠0），则下列各式正确的是（　　）

  A． a b = 4 3

  B． a b = 3 4

  C． a 3 = b 4

  D． a 3 = 4 b
  组卷：412引用：14难度：0.8

  解析

• 2．下列成语所描述的事件中，是随机事件的是（　　）

  A．水涨船高

  B．水中捞月

  C．一步登天

  D．一箭双雕
  组卷：117引用：4难度：0.7

  解析

• 3．已知抛物线y=ax²-2ax+3（a＞0），A（-1，y₁），B（2，y₂），C（4，y₃）是抛物线上三点，则y₁，y₂，y₃由小到大的排列是（　　）

  A．y1＜y2＜y3

  B．y2＜y1＜y3

  C．y3＜y1＜y2

  D．y2＜y3＜y1
  组卷：1992引用：18难度：0.5

  解析

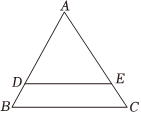• 4．如图，在△ABC中，D是AB边上一点，过点D作DE∥BC交AC于点E，若AD：DB=3：1，则S_△ADE：S_△ABC的值为（　　）

  A． 3 7

  B． 3 4

  C． 16 9

  D． 9 16
  组卷：454引用：4难度：0.5

  解析

• 5．如图，AB是半圆O的直径，∠BAC=28°，则∠D的度数是（　　）
  

  A．62°

  B．118°

  C．152°

  D．138°
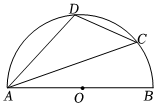  组卷：315引用：3难度：0.5

  解析

• 6．如图，在同一平面直角坐标系中，二次函数y=ax²+bx+c（a≠0）与一次函数y=acx+b的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：1840引用：10难度：0.5

  解析

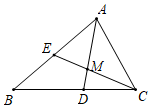• 7．如图，在△ABC中，AD是∠BAC的平分线，CE与AD交于点M，∠ACE=∠B，下列结论中不正确的是（　　）

  A．△ACM∽△ABD

  B．△ACE∽△ABC

  C．△AEM∽△CDM

  D．△AEM∽△ACD
  组卷：564引用：6难度：0.6

  解析

• 8．在平面直角坐标系中，有两条抛物线关于x轴对称，且它们的顶点相距8个单位长度．若其中一条抛物线的函数表达式为y=x²-6x+m,则m的值是（　　）

  A．-5或-13

  B．-1或19

  C．5或13

  D．4或14
  组卷：94引用：2难度：0.6

  解析

三、解答题

• 23．定义：若一个四边形能被其中的一条对角线分割成两个相似三角形，则称这个四边形为“师梅四边形”，这条对角线称为“师梅线”．我们熟知的平行四边形就是“师梅四边形”．
  
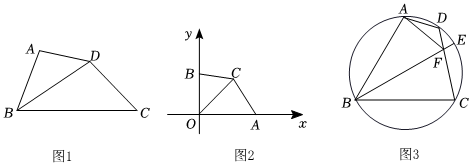
  （1）如图1，BD平分∠ABC，

  BD

  =

  4

  2

  ，BC=10．四边形ABCD是被BD分割成的“师梅四边形”，求AB长；
  （2）如图2，平面直角坐标系中，A、B分别是x轴和y轴上的点，且OA=3，OB=2，若点C是直线y=x在第一象限上的一点，且OC是四边形OACB的“师梅线”，求四边形OACB的面积；
  （3）如图3，圆内接四边形ABCD中，∠ABC=60°，点E是

  ˆ

  AC

  的中点，连接BE交CD于点F，连接AF，∠DAF=30°，
  ①求证：四边形ABCF是“师梅四边形”；
  ②若△ABC的面积为

  6

  3

  ，求线段BF的长．
  组卷：1167引用：9难度：0.1

  解析

• 24．已知抛物线y=x²+mx-2与x轴交于A、B两点，与y轴交于点C，点A坐标为（-2，0）
  
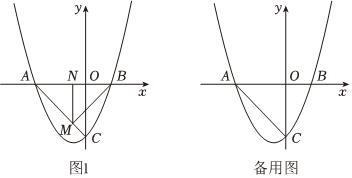
  （1）求抛物线的解析式及B、C两点的坐标．
  （2）若点M是线段AC上一个动点（不与A、C重合），点N是线段AB上一个动点，设AN=t（t＞0）．
  ①如图1，当点N运动到AB的中点时，作MN∥y轴交AC于点M．求证：∠BMN=∠BAC．
  ②当点N在运动过程中，在x轴上方的抛物线上是否存在点G，使得∠GNB=∠BAC且GN恰好平分∠AGB？若存在，求出此时点G的横坐标和t的值；若不存在，请说明理由．
  组卷：164引用：1难度：0.3

  解析