当前位置：试卷中心 > 试卷详情

2022-2023学年江西省吉安市井冈山市宁冈中学高三（上）月考数学试卷（文科）（12月份）

发布：2024/8/21 15:0:1

一、选择题（本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1．已知集合A={x|x²-3x-10＜0}，B={x|2^x＜2}，则A∩B=（　　）
A．（-2，1） B．（-5，1） C．∅ D．{0}
组卷：105引用：5难度：0.9
解析
2．已知点
P
（
1
2
，
1
）
是角α终边上一点，则sinα=（　　）
A．
5
5
B．
3
2
C．
1
2
D．
2
5
5
组卷：27引用：3难度：0.8
解析
3．20世纪30年代，查尔斯•里克特制定了一种表明地震能量大小的尺度，就是使用测震仪衡量地震能量的等级，地震能量越大，测震仪记录的地震曲线的振幅就越大．这就是我们常说的里氏震级M，其计算公式为M=lgA-lgA₀，其中，A是被测地震的最大振幅，A₀是“标准地震”的振幅（使用标准地震振幅是为了修正测震仪距实际震中的距离造成的偏差），则里氏7.5级地震的最大振幅余里氏4级地震的最大振幅的比值约为（　　）（参考数据：
10
≈
3
.
16
．）
A．790 B．1580 C．3160 D．6320
组卷：62引用：3难度：0.5
解析
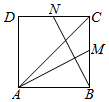4．如图，正方形ABCD中，M、N分别是BC、CD的中点，若
AC
=λ
AM
+μ
BN
，则λ+μ=（　　）
A．2 B．
8
3
C．
6
5
D．
8
5
组卷：3450引用：34难度：0.9
解析
5．已知
|
a
|
=
4
，
|
b
|
=
1
，
〈
a
，
b
〉
=
60
°
，则
|
a
-
2
b
|
等于（　　）
A．12 B．28 C．
2
3
D．
2
7
组卷：109引用：4难度：0.8
解析
6．已知α为第二象限角，sinα+cosα=
15
3
，则cos2α=（　　）
A．
-
5
3
B．
-
5
9
C．
5
3
D．
±
5
3
组卷：36引用：1难度：0.7
解析
7．给定实数x,定义[x]为不大于x的最大整数，则下列结论中不正确的是（　　）
A．x-[x]≥0
B．x-[x]＜1
C．令f（x）=x-[x]，对任意实数x,f（x+1）=f（x）恒成立
D．令f（x）=x-[x]，对任意实数x,f（-x）=f（x）恒成立
组卷：54引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共6小题，共70分．解答应写出必要的文字说明或推理、验算过程．）

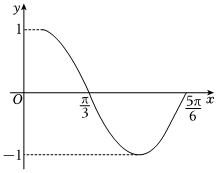21．如图是函数
f
（
x
）
=
A
sin
（
ωx
+
φ
）
（
A
＞
0
，
ω
＞
0
，
|
φ
|
＜
π
2
）
的部分图象．
（1）求函数f（x）的解析式；
（2）若cos⁴α-sin⁴α=
4
5
，
α
∈
（
0
，
π
2
）
，求f（α）．
组卷：93引用：2难度：0.5
解析
22．已知函数
f
（
x
）
=
（
x
2
+
x
）
ln
1
x
-
ax
，
g
（
x
）
=
2
3
x
3
+
（
1
-
a
）
x
2
-
2
ax
+
b
，a,b∈R．
（Ⅰ）求函数g（x）的单调区间；
（Ⅱ）若f（x）≤g（x）恒成立，求b-2a的最小值．
组卷：514引用：2难度：0.1
解析

0/60 进入组卷

0/20 进入试卷篮

布置作业 发布测评 反向细目表 平行组卷 下载答题卡 试卷分析 在线训练 收藏试卷

充值会员，资源免费下载

2022-2023学年江西省吉安市井冈山市宁冈中学高三（上）月考数学试卷（文科）（12月份）

一、选择题（本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1．已知集合A={x|x2-3x-10＜0}，B={x|2x＜2}，则A∩B=（ ）

2．已知点P（12，1）是角α终边上一点，则sinα=（ ）

4．如图，正方形ABCD中，M、N分别是BC、CD的中点，若AC=λAM+μBN，则λ+μ=（ ）

5．已知|a|=4，|b|=1，〈a，b〉=60°，则|a-2b|等于（ ）

6．已知α为第二象限角，sinα+cosα=153，则cos2α=（ ）

7．给定实数x,定义[x]为不大于x的最大整数，则下列结论中不正确的是（ ）

三、解答题（本大题共6小题，共70分．解答应写出必要的文字说明或推理、验算过程．）

21．如图是函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π2）的部分图象．（1）求函数f（x）的解析式；（2）若cos4α-sin4α=45，α∈（0，π2），求f（α）．

22．已知函数f（x）=（x2+x）ln1x-ax，g（x）=23x3+（1-a）x2-2ax+b，a,b∈R．（Ⅰ）求函数g（x）的单调区间；（Ⅱ）若f（x）≤g（x）恒成立，求b-2a的最小值．

1．已知集合A={x|x²-3x-10＜0}，B={x|2^x＜2}，则A∩B=（　　）

2．已知点
P
（
1
2
，
1
）
是角α终边上一点，则sinα=（　　）

4．如图，正方形ABCD中，M、N分别是BC、CD的中点，若
AC
=λ
AM
+μ
BN
，则λ+μ=（　　）

5．已知
|
a
|
=
4
，
|
b
|
=
1
，
〈
a
，
b
〉
=
60
°
，则
|
a
-
2
b
|
等于（　　）

6．已知α为第二象限角，sinα+cosα=
15
3
，则cos2α=（　　）

7．给定实数x,定义[x]为不大于x的最大整数，则下列结论中不正确的是（　　）

21．如图是函数
f
（
x
）
=
A
sin
（
ωx
+
φ
）
（
A
＞
0
，
ω
＞
0
，
|
φ
|
＜
π
2
）
的部分图象．
（1）求函数f（x）的解析式；
（2）若cos⁴α-sin⁴α=
4
5
，
α
∈
（
0
，
π
2
）
，求f（α）．

22．已知函数
f
（
x
）
=
（
x
2
+
x
）
ln
1
x
-
ax
，
g
（
x
）
=
2
3
x
3
+
（
1
-
a
）
x
2
-
2
ax
+
b
，a,b∈R．
（Ⅰ）求函数g（x）的单调区间；
（Ⅱ）若f（x）≤g（x）恒成立，求b-2a的最小值．