2022-2023学年陕西省西安市灞桥区铁一中陆港学校九年级（上）月考数学试卷（12月份）

一.选择题（共8小题，每小题3分，计24分）

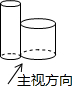• 1．如图所示的物体由两个紧靠在一起的圆柱体组成，它的左视图是（　　）

  A．

  B．

  C．

  D．
  组卷：271引用：13难度：0.9

  解析

• 2．下列函数中，是二次函数的是（　　）

  A．y=-4x+5	B．y=2x2-3x
  C．y=x（x+1）-x2	D．y= 1 x 2
  组卷：307引用：3难度：0.9

  解析

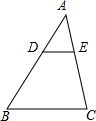• 3．如图，DE∥BC，AD：DB=2：3，EC=6，则AE的长是（　　）

  A．3

  B．4

  C．6

  D．10
  组卷：1045引用：14难度：0.9

  解析

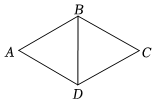• 4．如图，在菱形ABCD中，∠BAD=60°，对角线BD=6，则菱形的边AB的长为（　　）

  A．4

  B．6

  C．3 3

  D．8
  组卷：717引用：6难度：0.7

  解析

• 5．学生冬季运动装原来每套的售价是100元，后经连续两次降价，现在的售价是81元，则平均每次降价的百分数是（　　）

  A．9%

  B．8.5%

  C．9.5%

  D．10%
  组卷：237引用：34难度：0.9

  解析

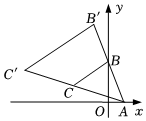• 6．如图所示，在直角坐标系中，A（1，0），B（0，2），以A为位似中心，把△ABC按相似比1：2放大，放大后的图形记作△AB'C'，则B'的坐标为（　　）

  A．（-1，-2）

  B．（-1，2）

  C．（-1，-4）

  D．（-1，4）
  组卷：289引用：3难度：0.6

  解析

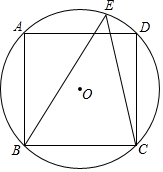• 7．如图，正方形ABCD内接于⊙O，点E在

  ˆ

  AD

  上，则∠BEC的度数（　　）

  A．25°

  B．50°

  C．45°

  D．100°
  组卷：369引用：4难度：0.6

  解析

• 8．已知二次函数y=ax²+bx+c（a,b,c是常数，a≠0）的y与x的部分对应值如表：

  x	-5	-4	-2	0	2
  y	6	0	-6	-4	6

  则下列说法正确的是（　　）

  A．a＜0

  B．当x=-2时，函数最小值为-6

  C．若点（-8，y1），点（8，y2）在二次函数图象上，y1＞y2

  D．方程ax2+bx+c+5=0有两个不相等的实数根
  组卷：52引用：2难度：0.5

  解析

三.解答题（共12小题，计81分）

• 24．已知抛物线

  y

  =

  -

  1

  2

  x

  2

  +

  bx

  +

  c

  与x轴交于A（-1，0），B（4，0）两点，与y轴交于点C．
  （1）求该抛物线的表达式；
  （2）求△ABC的面积；
  （3）在抛物线上是否存在一点P，使tan∠BAP=1，若存在，求出点P的坐标，若不存在，请说明理由．
  组卷：56引用：2难度：0.5

  解析

• 25．【问题提出】
  
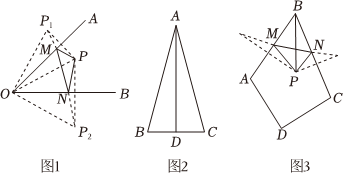
  （1）如图1，∠AOB=45°，在∠AOB内部有一点P，M、N分别是OA、OB上的动点，分别作点P关于边OA、OB的对称点P₁，P₂，连接P₁，P₂与OA、OB相交于M、N，则此时△PMN的周长最小，且顺次连接O，P₁，P₂后△OP₁P₂的形状是等腰直角三角形．理由如下：
  ∵点P关于边OA、OB的对称点分别为P₁，P₂，
  ∴OP=OP₁=OP₂，∠AOP=∠AOP₁，∠BOP=∠BOP₂，PM=P₁M，PN=P₂N．
  ∴C_△PMN=PM+PN+MN=P₁M+P₂N+MN=P₁P₂，
  即△PMN周长的最小值为P₁P₂．
  ∵∠AOB=45°，
  ∴∠P₁OP₂=2（∠AOP+∠BOP）=90°．
  ∴△OP₁P₂是等腰直角三角形．
  学以致用：若∠AOB=30°，在∠AOB内部有一点P，分别作点P关于边OA、OB的对称点P₁，P₂，顺次连接O，P₁，P₂，则△OP₁P₂的形状是

  三角形．
  （2）【问题探究】如图2，在△ABC中，AB=AC，∠BAC=30°，点D是BC的中点，若AD=h,请用含有h的代数式表示△ABC的面积．
  （3）【问题解决】如图3，在四边形ABCD内有一点P，点P到顶点B的距离为10，∠ABC=60°，点M、N分别是AB、BC边上的动点，顺次连接P、M、N，使△PMN在周长最小的情况下，面积最大，问：是否存在使△PMN在周长最小的条件下，面积最大这种情况？若存在，请求出△PMN的面积的最大值；若不存在，请说明理由．
  组卷：181引用：2难度：0.2

  解析