2023-2024学年江苏省南京市浦口区明道学校八年级（上）月考数学试卷（10月份）

一、选择题（共8题，每题2分）

• 1．下列图形中，不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：102引用：11难度：0.9

  解析

• 2．图中的两个三角形全等，则∠α等于（　　）
  

  A．65°

  B．60°

  C．55°

  D．50°
  组卷：551引用：10难度：0.7

  解析

• 3．到三角形三个顶点距离都相等的点是（　　）

  A．三角形的三条角平分线的交点

  B．三角形的三边垂直平分线的交点

  C．三角形的三条高线的交点

  D．三角形的三条中线的交点
  组卷：532引用：7难度：0.7

  解析

• 4．等腰三角形两边长分别为2和4，则这个等腰三角形的周长为（　　）

  A．6

  B．8

  C．10

  D．8或10
  组卷：852引用：15难度：0.6

  解析

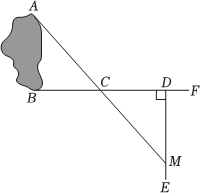• 5．如图是嘉淇测量水池AB宽度的方案，下列说法不正确的是（　　）
  ①先确定直线AB，过点B作BF⊥AB；
  ②在BF上取C，D两点，使得△；
  ③过点D作DE⊥BF；
  ④作射线□，交DE于点M；
  ⑤测量☆的长度，即AB的长．

  A．△代表BC=CD	B．□代表AC
  C．☆代表DM	D．该方案的依据是SAS
  组卷：845引用：11难度：0.5

  解析

• 6．如图，在3×3的正方形网格中有两个小正方形被涂黑，再将图中其余小正方形任意一个涂黑，使得整个图形（包括网格）构成一个轴对称图形，那么涂法共有（　　）

  A．3种

  B．4种

  C．5种

  D．6种
  组卷：469引用：4难度：0.7

  解析

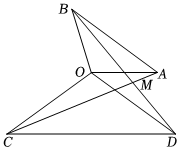• 7．如图，在△AOB和△COD中，OA=OB，OC=OD，∠AOB=∠COD，AC，BD交于点M，关于结论Ⅰ，Ⅱ，下列判断正确的是（　　）
  结论Ⅰ：AC=BD；
  结论Ⅱ：∠CMD＞∠COD

  A．Ⅰ对，Ⅱ错

  B．Ⅰ错，Ⅱ对

  C．1，Ⅱ都对

  D．Ⅰ，Ⅱ都错
  组卷：1031引用：6难度：0.5

  解析

• 8．如图，∠ABC=60°，AB=6，动点P从点B出发，以每秒1个单位长度的速度沿射线l运动，设点P的运动时间为t秒（t＞0），当△ABP为锐角三角形时，t的取值范围是（　　）

  A．t＞3

  B．t＞6

  C．6＜t＜12

  D．3＜t＜12
  组卷：649引用：4难度：0.5

  解析

三、解答题

• 25．如图①，△ABC和△CDE是等边三角形，连接AE、BD，连接DA并延长交BC于点F，AE=CE．
  （1）求证：△DBC≌△EAC；
  （2）如图②，作△ADE的边AD上的高线EG，交BA的延长线于点P，求证：PB=PE．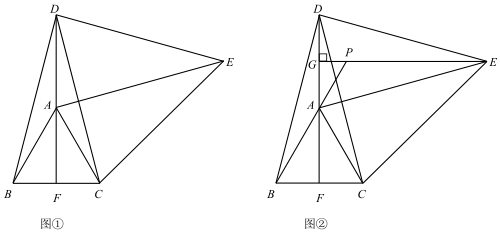
  
  组卷：771引用：5难度：0.5

  解析

• 26．在边长为9的等边三角形ABC中，点Q是BC上一点，点P是AB上一动点，以1个单位每秒的速度从点A向点B移动，设运动时间为t秒．
  （1）如图1，若BQ=6，PQ∥AC求t的值；
  （2）如图2，若点P从点A向点B运动，同时点Q以2个单位的速度从点B经点C向点A运动，当t为何值时，△APQ为等边三角形．
  （3）如图3，将边长为9的等边三角形ABC变换为AB，AC为腰，BC为底的等腰三角形，且AB=AC=10，BC=8，点P运动到AB中点处静止，点M，N分别为BC，AC上动点，点M以1个单位每秒的速度从点B向C运动，同时N以a个单位每秒的速度从点C向A运动，当△BPM，△CNM全等时，求a的值．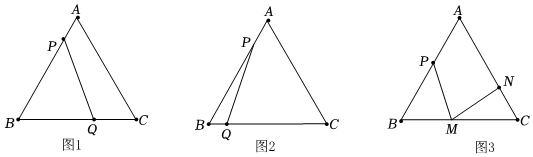
  
  组卷：263引用：4难度：0.3

  解析