当前位置：试卷中心 > 试卷详情

2022-2023学年安徽省芜湖市无为市七年级（下）期中数学试卷

发布：2024/6/24 8:0:9

一、单选题（共40分）

1．在实数
22
7
，-
9
，
π
2
，1.414，3，0.1010010001…（每两个1之间0的个数依次增加1）中，无理数有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：40引用：1难度：0.8
解析
2．按下列语句画图：点A在直线m上，也在直线n上，但不在直线c上，且直线m、n、c两两相交，下列图形符合题意的是（　　）
A． B． C． D．
组卷：319引用：3难度：0.8
解析
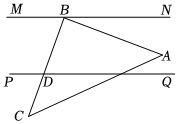3．如图，MN∥PQ，将一块三角板ABC如图所示放置，∠ABC=90°，∠BDQ=70°，则∠ABN的度数为（　　）
A．10° B．20° C．30° D．40°
组卷：626引用：3难度：0.6
解析
4．下列命题中，是真命题的是（　　）
A．两个锐角的和是锐角
B．邻补角是互补的角
C．同旁内角互补
D．两条直线被第三条直线所截，内错角相等
组卷：281引用：8难度：0.9
解析
5．在数轴上与表示
11
的点距离最近的整数点所表示的数为（　　）
A．1 B．2 C．3 D．4
组卷：144引用：3难度：0.8
解析
6．在平面直角坐标系xOy中，已知点A（4，-2），B（-2，-2），下列说法：①直线AB∥x轴；②点A与点B的距离为6个单位长度；③点B到两坐标轴的距离相等；④连接OA，OB，则∠AOB为钝角；其中错误的说法的个数是（　　）
A．0 B．1 C．3 D．4
组卷：386引用：3难度：0.7
解析
7．在实数范围内，下列判断正确的是（　　）
A．若|m|=|n|，则m=n B．若a²＞b²，则a＞b
C．若
a
2
=
（
b
）
2
，则a=b D．若
3
a
=
3
b
，则a=b
组卷：255引用：4难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（共90分）

22．在平面直角坐标系xOy中，给出如下定义：点A到x轴、y轴距离的较小值称为点A的“短距”，当点P的“短距”等于点Q的“短距”时，称P、Q两点为“等距点”．
（1）点A（-5，-2）的“短距”为
；
（2）点B（-2，-2m+1）的“短距”为1，求m的值；
（3）若C（-1，k+3），D（4，2k-3）两点为“等距点”，求k的值．
组卷：1032引用：12难度：0.8
解析
23．在平面直角坐标系中，有点A（m,0），B（0，n），且m,n满足m=
n
2
-
1
+
1
-
n
2
-
4
n
+
1
．

（1）求A、B两点坐标；
（2）如图1，直线l⊥x轴，垂足为点Q（1，0）．点P为直线l上任意一点，且点P在第四象限，若△PAB的面积为
7
2
，求点P的坐标；
（3）如图2，点D为y轴负半轴上一点，过点D作CD∥AB，E为线段AB上任意一点，以O为顶点作∠EOF，使∠EOF=90°，OF交CD于F．点G为线段AB与线段CD之间一点，连接GE，GF，∠AEG=
1
3
∠
AEO
．当点E在线段AB上运动时，EG始终垂直于GF，试写出∠CFG与∠GFO之间的数量关系，并证明你的结论
组卷：116引用：1难度：0.1
解析