2022-2023学年浙江省台州市仙居县白塔中学九年级（上）期中数学试卷

一、选择题（本大题共10小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

• 1．下列关于防范“新冠肺炎”的标志中既是轴对称图形，又是中心对称图形的是（　　）

  A． 戴口罩讲卫生	B． 勤洗手勤通风
  C． 有症状早就医	D． 少出门少聚集
  组卷：2708引用：65难度：0.9

  解析

• 2．平移抛物线y=（x+3）（x-1）后得到抛物线y=（x+1）（x-3），则（　　）

  A．向左平移2个单位	B．向右平移2个单位
  C．向左平移4个单位	D．向右平移4个单位
  组卷：321引用：7难度：0.6

  解析

• 3．下列方程为一元二次方程的是（　　）

  A．2x-1=0

  B．x2-4x+4=0

  C．xy-1=0

  D．x2+2x+1
  组卷：32引用：4难度：0.8

  解析

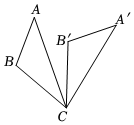• 4．如图，将△ABC绕着点C顺时针旋转50°后得到△A'B'C．若∠A=40°，∠B'=110°，则∠BCA'的度数为（　　）

  A．30°

  B．50°

  C．80°

  D．90°
  组卷：460引用：9难度：0.7

  解析

• 5．有一个人患流感，经过两轮传染后共有81个人患流感，每轮传染中平均一个人传染几个人？设每轮传染中平均一个人传染x个人，可列方程为（　　）

  A．1+2x=81	B．1+x2=81
  C．1+x+x2=81	D．1+x+x（1+x）=81
  组卷：3901引用：23难度：0.6

  解析

• 6．将△ABC的三个顶点的横坐标乘以-1，纵坐标不变，则所得图形与原图的关系是（　　）

  A．关于x轴对称

  B．关于y轴对称

  C．关于原点对称

  D．将原图的x轴的负方向平移了了1个单位
  组卷：711引用：12难度：0.8

  解析

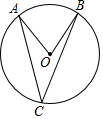• 7．如图，点A，B，C在⊙O上，∠AOB=72°，则∠ACB等于（　　）

  A．28°

  B．54°

  C．18°

  D．36°
  组卷：2058引用：33难度：0.7

  解析

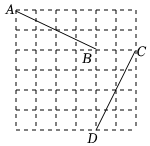• 8．如图，在正方形网格中，线段AB绕点O旋转一定的角度后与线段CD重合（C、D均为格点，A的对应点是点C），若点A的坐标为（-1，5），点B的坐标为（3，3），则旋转中心O点的坐标为（　　）

  A．（1，1）	B．（4，4）
  C．（2，1）	D．（1，1）或（4，4）
  组卷：879引用：7难度：0.6

  解析

四、解答题（本大题共7小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

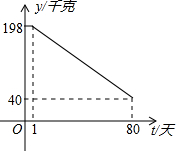• 23．某水产养殖户进行小龙虾养殖．已知每千克小龙虾养殖成本为6元，在整个销售旺季的80天里，销售单价P（元/千克）与时间第t（天）之间的函数关系为：P=

  1 4 t + 16 （ 1 ≤ t ≤ 40 ， t 为整数 ）

  - 1 2 t + 46 （ 41 ≤ t ≤ 80 ， t 为整数 ）

  ，日销售量y（千克）与时间第t（天）之间的函数关系如图所示：
  （1）求日销售量y与时间t的函数关系式？
  （2）哪一天的日销售利润最大？最大利润是多少？
  （3）在实际销售的前40天中，该养殖户决定每销售1千克小龙虾，就捐赠m（m＜7）元给村里的特困户．在这前40天中，每天扣除捐赠后的日销售利润随时间t的增大而增大，求m的取值范围．
  组卷：841引用：9难度：0.3

  解析

• 24．【问题背景】
  如图1，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，探究线段AC，BC，CD之间的数量关系．
  小吴同学探究此问题的思路是：将△BCD绕点D，逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图2），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=

  2

  CD，从而得出结论：AC+BC=

  2

  CD
  【简单应用】
  （1）在图1中，若AC=

  2

  ，BC=2

  2

  ，则CD=

  ．
  （2）如图3，AB是⊙O的直径，点C、D在⊙O上，

  ˆ

  AD

  =

  ˆ

  BD

  ，若AB=13，BC=12，求CD的长．
  【拓展规律】
  （3）如图4，∠ACB=∠ADB=90°，AD=BD，若AC=m,BC=n（m＜n），求CD的长（用含m,n的代数式表示）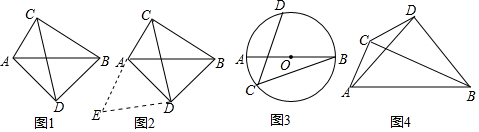
  
  组卷：624引用：15难度：0.1

  解析