当前位置：试卷中心 > 试卷详情

2022-2023学年广东省佛山市高明区初中教学联盟八年级（下）第二次月考数学试卷

发布：2024/5/23 8:0:8

一.单选题（本大题共10小题，每小题3分，共30分）

1．若分式
x
2
x
+
10
有意义，则x的取值范围是（　　）
A．x≠0 B．x≠5 C．x≠-5 D．x≠-10
组卷：472引用：5难度：0.5
解析
2．全国各地都在实施垃圾分类回收．下列图形分别是可回收物、厨余垃圾、有害垃圾及其它垃圾的标志，其中，既是中心对称图形又是轴对称图形的是（　　）
A． B． C． D．
组卷：185引用：7难度：0.8
解析
3．若a＜b,则下列各式一定成立的是（　　）
A．a-1＞b-1 B．-3a＜-3b C．4a＞4b D．a+2＜b+2
组卷：38引用：2难度：0.6
解析
4．多项式8a²b+4ab中各项的公因式是（　　）
A．ab B．4ab C．8a²b D．8a³b²
组卷：725引用：4难度：0.8
解析

5．下列说法，正确的是（　　）

A．一个三角形两边的垂直平分线的交点到这个三角形三边的距离相等

B．“若a＞b,则a²＞b²”的逆命题是真命题

C．在角的内部到角的两边距离相等的点一定在这个角的平分线上

D．用反证法证明“三角形中必有一个角不大于60°”，先假设这个三角形中有一个内角大于60°

组卷：1315引用：11难度：0.7

解析

6．下列因式分解中，正确的是（　　）
A．2a³-4a²+2a=2a（a²-2a） B．
a
2
-
a
+
1
4
=
（
a
-
1
2
）
2
C．a³-9a=a（a²-9） D．-a²-b²=-（a+b）（a-b）
组卷：487引用：6难度：0.7
解析
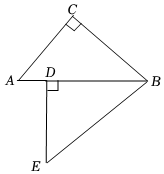7．如图，在Rt△ABC中，∠C=90°，∠A=55°，点D在斜边AB上，如果把△ABC绕点B逆时针旋转后与△EBD重合，那么旋转角等于（　　）
A．35° B．55° C．80° D．90°
组卷：62引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三．解答题（第16-18题每题8分，第19-21题每题9分，第22-23题每题12分，共75分）

22．教材中这样写道：“我们把多项式a²+2ab+b²及a²-2ab+b²叫做完全平方式”，如果关于某一字母的二次多项式不是完全平方式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，不仅可以将一个看似不能分解的多项式分解因式，还能解决一些与非负数有关的问题或求代数式最大值，最小值等．
例如：分解因式x²+2x-3．
原式=（x²+2x+1）-4=（x+1）²-4=（x+1+2）（x+1-2）=（x+3）（x-1）；
例如：求代数式x²+4x+6的最小值．
原式=x²+4x+4+2=（x+2）²+2．
∵（x+2）²≥0，
∴当x=-2时，x²+4x+6有最小值是2．
根据阅读材料用配方法解决下列问题：
（1）分解因式：m²-4m-5=
；
（2）求代数式x²-6x+12的最小值；
（3）若y=-x²+2x-3，当x=
时，y有最
值（填“大”或“小”），这个值是
；
（4）当a,b,c分别为△ABC的三边时，且满足a²+b²+c²-6a-10b-8c+50=0时，判断△ABC的形状并说明理由．
组卷：810引用：4难度：0.5
解析
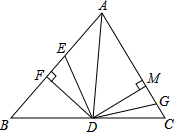23．如图，在△ABC中，∠BAD=∠DAC，DF⊥AB，DM⊥AC，AF=10厘米，AC=14厘米，动点E以4厘米/秒的速度从A点向F点运动，动点G以2厘米/秒的速度从C点向A点运动，当一个点到达终点时，另一个点随之停止运动，设运动时间为t秒．
（1）求证：AF=AM；
（2）求证：在运动过程中，不管t取何值，都有S_△AED=2S_△DGC；
（3）当t取何值时，△DFE与△DMG全等．
组卷：531引用：7难度：0.3
解析