2022-2023学年湖南省怀化市溆浦一中八年级（上）期中数学试卷

一、单选题（共40分）

• 1．下列各式中，是分式的有（　　）
  -

  3

  2

  x,

  4

  x

  -

  y

  ，x+y,

  x

  2

  +

  1

  π

  ，

  7

  8

  ，

  5

  b

  3

  a

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：206引用：14难度：0.9

  解析

• 2．以下列各组线段长为边能组成三角形的是（　　）

  A．1cm,2cm,4cm	B．2cm,4cm,6cm
  C．4cm,6cm,8cm	D．5cm,6cm,12cm
  组卷：661引用：9难度：0.9

  解析

• 3．已知某新型感冒病毒的直径约为0.000 000 733米，将0.000 000 733用科学记数法表示为（　　）

  A．7.33×10-6

  B．7.33×10-7

  C．7.33×106

  D．7.33×107
  组卷：134引用：4难度：0.8

  解析

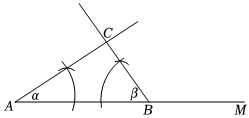• 4．如图是作△ABC的作图痕迹，则此作图的已知条件是（　　）

  A．已知两边及夹角	B．已知三边
  C．已知两角及夹边	D．已知两边及一边对角
  组卷：1720引用：30难度：0.5

  解析

• 5．如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P₁，P₂，P₃，P₄四个点中找出符合条件的点P，则点P有（　　）

  A．1个

  B．2个

  C．3个

  D．4个
  组卷：10841引用：185难度：0.9

  解析

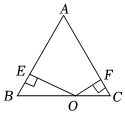• 6．如图，△ABC是等腰三角形，点O是底边BC上任意一点，OE、OF分别与两边垂直，等腰三角形ABC的腰长为4，面积为10，则OE+OF的值为（　　）

  A．10

  B．8

  C．7

  D．5
  组卷：46引用：3难度：0.5

  解析

• 7．如果x²+2x-2=0，那么代数式

  1

  x

  -

  2

  •

  x

  2

  -

  4

  x

  +

  4

  x

  -

  x

  x

  +

  2

  的值为（　　）

  A．-2

  B．-1

  C．1

  D．2
  组卷：785引用：8难度：0.7

  解析

• 8．如图，在等腰△ABC中，AB=AC，∠BAC=50°．∠BAC的平分线与线段AB的中垂线交于点O，点C沿EF折叠后与点O重合，则∠CEF的度数是（　　）

  A．45°

  B．50°

  C．55°

  D．60°
  组卷：976引用：12难度：0.7

  解析

三、解答题（共86分）

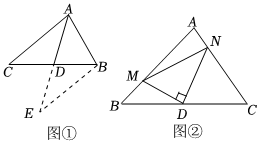• 23．（1）阅读理解：
  如图①，在△ABC中，若AB=8，AC=12，求BC边上的中线AD的取值范围，并说明理由．
  解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB、AC，2AD集中在△ABE中，体现了转化和化归的数学思想，利用三角形三边的关系即可判断．
  （2）问题解决：
  如图②，在△ABC中，D是BC边上的中点，DM⊥DN于点D，DM交AB于点M，DN交AC于点N，连接MN，求证：BM+CN＞MN．
  组卷：226引用：2难度：0.5

  解析

• 24．如图1．等腰△ABC中，AB=AC．点D是AC上一动点，点E在BD延长线上．且AB=AE．CF=EF．
  （1）在图1中，证明：∠BFC=∠BAC；
  （2）若∠BAC=60°，如图2．探究线段AF、BF、EF之间的数量关系，并证明；
  （3）若∠BAC=90°且BD平分∠ABC，如图3．求

  EF

  BD

  的值．
  
  组卷：568引用：5难度：0.1

  解析