当前位置：试卷中心 > 试卷详情

2023-2024学年北京四中九年级（上）开学数学试卷

发布：2024/8/3 8:0:9

一.选择题（每题2分，共16分）

1．下列各式是最简二次根式的是（　　）
A．
9
B．
25
2
C．
6
D．
50
组卷：161引用：2难度：0.8
解析
2．下列各组数中，不能构成直角三角形的是（　　）
A．1，2，3 B．3，4，5 C．5，12，13 D．7，24，25
组卷：265引用：4难度：0.8
解析
3．下列化简正确的是（　　）
A．
4
+
9
=
13
B．
12
=
2
3
C．
-
（
-
3
）
2
=
3
D．
3
2
-
2
=
3
组卷：537引用：6难度：0.6
解析
4．菱形和平行四边形都具有的性质是（　　）
A．对角线相等 B．对角线互相垂直
C．对角线平分一组对角 D．对角线互相平分
组卷：377引用：3难度：0.5
解析
5．在平面直角坐标系xOy中，点A（2，y₁），B（3，y₂）在函数y=-7x-4的图象上，则（　　）
A．y₁＞y₂ B．y₁=y₂
C．y₁＜y₂ D．以上都有可能
组卷：448引用：3难度：0.8
解析
6．如图是甲、乙两名同学五次数学测试成绩的折线图．比较甲、乙两名同学的成绩，下列说法正确的是（　　）
A．甲同学平均分高，成绩波动较小
B．甲同学平均分高，成绩波动较大
C．乙同学平均分高，成绩波动较小
D．乙同学平均分高，成绩波动较大
组卷：364引用：9难度：0.7
解析
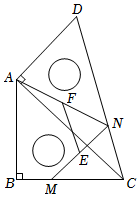7．一副三角板如图放置，等腰直角三角板的斜边与含30°的直角三角板长直角边重合于AC，∠B=∠CAD=90°，∠ACD=30°，AB=BC，点N在边CD上运动，点M在边BC上运动，连接MN，AN，分别作出MN和AN边的中点E和F，测得EF的最小值是6cm,则最长的斜边CD的长为（　　）
A．3
6
cm B．8
2
cm C．8
3
cm D．8
6
cm
组卷：261引用：2难度：0.6
解析
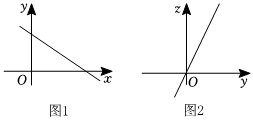8．图1是变量y与变量x的函数关系的图象，图2是变量z与变量y的函数关系的图象，则z与x的函数关系的图象可能是（　　）
A． B． C． D．
组卷：1301引用：18难度：0.7
解析

二.填空题（每题2分，共16分）

9．若
x
-
5
在实数范围内有意义，则实数x的取值范围是
．
组卷：1133引用：67难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（17、18、21、23、25、26、27每题6分，19题4分，20、22、24每题5分，28题7分，共68分）

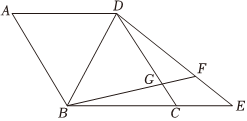26．如图，在菱形ABCD中，∠A=60°，点E为BC延长线上一点．连接DE，在线段DE上取点F使∠FBE=
1
2
∠CDE，点G为FB与CD的交点．求证：
（1）FD=AD；
（2）请写出线段GC、CE、EF之间的数量关系，并证明．
组卷：192引用：1难度：0.6
解析
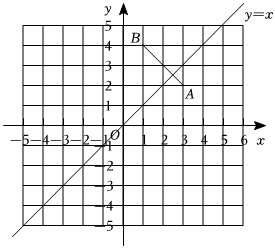27．如图，在平面直角坐标系xOy中，对于线段AB和点Q，给出如下定义：若在直线y=x上存在点P，使得四边形ABPQ为平行四边形，则称点Q为线段AB的“银杏点”．已知A（3，2），B（1，4）．
（1）在Q₁（-1，3），Q₂（-2，-6），Q₃（2，-2），Q₄（4，4）中，线段AB的“银杏点”是
；
（2）点Q为直线y=kx-2上一点，若点Q是线段AB的“银杏点”且不在第四象限，求k的取值范围；
（3）已知正方形CDEF边长为1，以T（2，t）为中心且各边与坐标轴垂直或平行，点M，N在线段AB上．若正方形CDEF上的任意一点都存在线段MN，使得该点为线段MN的“银杏点”，直接写出t的取值范围．
组卷：102引用：1难度：0.3
解析