当前位置：试卷中心 > 试卷详情

2022-2023学年内蒙古阿拉善盟高一（下）期末数学试卷

发布：2024/7/28 8:0:9

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．已知复数
z
=
i
2022
1
+
2
i
（i是虚数单位），则z在复平面内对应的点位于（　　）
A．第一象限 B．第二象限 C．第三象限 D．第四象限
组卷：68引用：5难度：0.8
解析
2．已知向量
a
=（k,3），
b
=（1，4），
c
=（2，1）且（2
a
-3
b
）⊥
c
，则实数k=（　　）
A．-
9
2
B．0 C．3 D．
15
2
组卷：4265引用：74难度：0.9
解析
3．下列说法正确的是（　　）
A．若
|
a
|
=
|
c
|
，则
a
=
c
B．若
a
∥
b
，则存在唯一实数λ使得
a
=
λ
b
C．若
a
∥
b
，
b
∥
c
，则
a
∥
c
D．与非零向量
a
共线的单位向量为
±
a
|
a
|
组卷：438引用：3难度：0.5
解析
4．已知
sin
（
α
+
π
3
）
=
3
5
，则
sin
（
2
α
+
π
6
）
=（　　）
A．
24
25
B．
-
24
25
C．
7
25
D．
-
7
25
组卷：850引用：11难度：0.7
解析
5．已知向量
a
，
b
满足
|
a
|
=
2
，
|
b
|
=
3
，
|
a
-
2
b
|
=
2
7
，则
a
与
b
所成角为（　　）
A．
5
π
6
B．
2
3
π
C．
π
3
D．
π
6
组卷：123引用：4难度：0.6
解析
6．工厂为了了解某车间的生产效率，对该车间200名工人上月生产的产品数量（单位：件）进行抽样调查，整理得到如图的频率分布直方图，则下列估计正确的为（　　）
①该车间工人上月产量的极差恰好为50件；
②车间约有120名工人上月产量低于65件；
③该车间工人上月产量的平均数低于64件；
④该车间工人上月产量的中位数低于63件．
A．①③ B．①④ C．②③ D．②④
组卷：44引用：4难度：0.7
解析
7．已知正三棱锥S-ABC的所有棱长均为2，则侧面与底面所成二面角的余弦值为（　　）
A．
2
2
3
B．-
2
2
3
C．
1
3
D．-
1
3
组卷：356引用：5难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

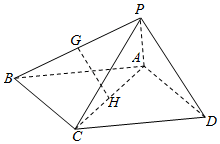21．如图，在四棱锥P-ABCD中，底面ABCD为平行四边形，△PCD为等边三角形，平面PAC⊥平面PCD，PA⊥CD，CD=2，AD=3．
（Ⅰ）设G，H分别为PB，AC的中点，求证：GH∥平面PAD；
（Ⅱ）求证：PA⊥平面PCD；
（Ⅲ）求直线AD与平面PAC所成角的正弦值．
组卷：5661引用：27难度：0.4
解析
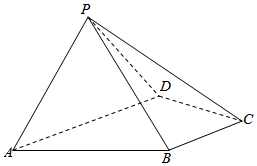22．如图，四棱锥中P-ABCD，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，PA=PD，AD=2BC．
（Ⅰ）证明：平面PAD⊥平面PCD；
（Ⅱ）若△PAB是面积为
3
的等边三角形，求四棱锥P-ABCD的体积．
组卷：277引用：4难度：0.5
解析