2022-2023学年湖北省荆州市监利市高二(下)月考数学试卷(2月份)
发布:2024/7/21 8:0:9
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
-
1.在一次抛硬币的试验中,某同学用一枚质地均匀的硬币做了1000次试验,发现正面朝上出现了560次,那么出现正面朝上的频率和概率分别为( )
组卷:124引用:2难度:0.7 -
2.若直线经过两点A(m,1),B(2-3m,2),且其倾斜角为135°,则m的值为( )
组卷:716引用:2难度:0.7 -
3.圆O1:(x-2)2+y2=4与圆O2:(x-4)2+y2=16的位置关系为( )
组卷:168引用:2难度:0.8 -
4.已知双曲线C:
的离心率为2,且与椭圆x2a2-y2b2=1(a>0,b>0)=1有公共焦点,则双曲线C的方程为( )x29+y25组卷:59引用:2难度:0.7 -
5.足球点球大战中,每队派出5人进行点球,假设甲队每人点球破门的概率都是
,乙队每人点球破门的概率都是34,若甲队进4球的概率为P1,乙队队进3球的概率为P2,则( )23组卷:91引用:3难度:0.8 -
6.已知三棱锥O-ABC中,
,AM=13AB,且CN=13CO,OA=a,OB=b,则OC=c=( )NM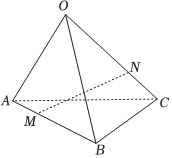 组卷:783引用:5难度:0.5
组卷:783引用:5难度:0.5 -
7.记等差数列{an}的前n项和为Sn,已知S5=15,a4=5,则S10=( )
组卷:89引用:2难度:0.7
四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.
-
21.过抛物线C:x2=2py(p>0)的焦点F且垂直于y轴的直线与C交于M,N两点(M在第一象限),O为坐标原点,△OMN的面积为2.
(1)求抛物线C的方程;
(2)设过点(-2,-3)的直线l与抛物线C相交于A,B两点(异于点M),设直线MA,MB的斜率分别为k1,k2,证明:k1k2为定值.组卷:49引用:2难度:0.4 -
22.已知椭圆C:
的上顶点为K,左右顶点分别为A,B,tan∠KAB=x2a2+y2b2=1(a>b>0),△KAB的周长为4+212.5
(1)求椭圆C的方程;
(2)O为坐标原点,O,B关于直线L对称,过直线L与x轴的交点作斜率为k的直线l与椭圆C交于不同的两点M,N(异于A,B两点),直线AM,AN分别交直线L于P,Q两点,当四边形APBQ的面积为4时,求k的值.组卷:16引用:2难度:0.5


