当前位置：试卷中心 > 试卷详情

2022-2023学年重庆市缙云教育联盟高三（上）质检数学试卷（11月份）

发布：2024/6/22 8:0:10

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．设集合A={x|log₂x≤0}，B={x|1＜3^x≤27}，则（∁_RA）∩B=（　　）
A．（0，1） B．（1，3] C．（1，3） D．[1，3）
组卷：68引用：3难度：0.7
解析
2．已知a=1.1^1.1，b=e^0.11，c=1+1.1ln1.1，下列说法正确的是（　　）
A．a＞b＞c B．b＞c＞a C．b＞a＞c D．a＞c＞b
组卷：87引用：6难度：0.7
解析
3．在△ABC中，角A，B，C所对的边分别为a,b,c,
∠
A
=
π
3
，AD是∠A的平分线，
AD
=
3
，AB＞1，则b+2c的最小值是（　　）
A．6 B．
3
-
2
2
C．
3
+
2
2
D．10
组卷：145引用：3难度：0.6
解析
4．购买同一种物品，可以用两种不同的策略，第一种是不考虑物品价格的升降，每次购买这种物品的数量一定；第二种是不考虑物品价格的升降，每次购买这种物品所花的钱一定．假设连续购买两天该物品，第一天物品的价格为a₁，第二天物品的价格为a₂，且a₁≠a₂，则以下选项正确的为（　　）
A．第一种方式购买物品的单价为
1
1
a
1
+
1
a
2
B．
2
1
a
1
+
1
a
2
≥
a
1
+
a
2
2
C．第一种购买方式所用单价更低
D．第二种购买方式所用单价更低
组卷：6引用：3难度：0.6
解析
5．数列{a_n}满足
a
1
=
2
，
a
n
+
1
=
2
（
n
+
2
）
n
+
1
a
n
（
n
∈
N
*
）
，则
a
2022
a
1
+
a
2
+
...
+
a
2021
=（　　）
A．
2022
2021
B．
2023
2021
C．
2021
2022
D．
2022
2023
组卷：187引用：5难度：0.5
解析
6．已知矩形ABCD的对角线交于点O，E为AO的中点，若
DE
=
λ
AB
+
μ
AD
（λ，μ为实数），则λ²-μ²=（　　）
A．
-
1
2
B．
7
9
C．
3
-
2
2
2
D．
1
+
2
2
组卷：127引用：4难度：0.7
解析
7．高斯是德国著名的数学家，近代数学奠基者之一，享有“数学王子”的称号．用他的名字定义的函数称为高斯函数f（x）=[x]，其中[x]表示不超过x的最大整数，已知数列{a_n}满足a₁=2，a₂=6，a_n+2+5a_n=6a_n+1，若b_n=[log₅a_n+1]，为数列
{
1000
b
n
b
n
+
1
}
的前n项和，则[S₂₀₂₄]=（　　）
A．999 B．749 C．499 D．249
组卷：194引用：6难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

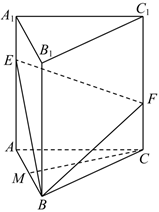21．如图，正三棱柱ABC-A₁B₁C₁中，E，F分别是棱AA₁，CC₁上的点，CM∥平面BEF，且M是AB的中点．
（1）证明：平面BEF⊥平面ABB₁A₁；
（2）若AC=AE，求平面BEF与平面BCE夹角的余弦值．
组卷：27引用：4难度：0.4
解析
22．已知函数f（x）=x²+x-1，α，β是方程f（x）=0的两个根（α＞β），f′（x）是f（x）的导数，设a₁=1，
a
n
+
1
=
a
n
-
f
（
a
n
）
f
′
（
a
n
）
（n=1，2，…）．
（1）求α，β的值；
（2）证明：对任意的正整数n,都有a_n＞α；
（3）记
b
n
=
ln
a
n
-
β
a
n
-
α
（n=1，2，…），求数列{b_n}的前n项和S_n．
组卷：474引用：11难度：0.1
解析