2023年广东省深圳市建文外国语学校高考数学一模试卷

一、单项选择题：本大题共8小题，每小题5分，满分40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={x∈Z|x²-3≤0}，B={1，2}，则A∪B=（　　）

  A．{0，1，2}	B．{-2，-1，0，1，2}
  C．{-2，-1，1，2}	D．{-1，0，1，2}
  组卷：336引用：8难度：0.8

  解析

• 2．已知复数z满足z（1+i）=i²⁰²³，其中i为虚数单位，则z的虚部为（　　）

  A． - 1 2

  B． 1 2

  C． - 1 2 i

  D． 2 2
  组卷：185引用：4难度：0.8

  解析

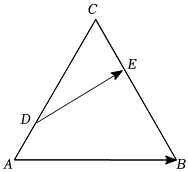• 3．如图所示，边长为2的正三角形ABC中，

  BD

  =

  BA

  +

  1

  3

  AC

  ，

  AE

  =

  AC

  +

  1

  3

  CB

  ，则

  DE

  •

  AB

  =（　　）

  A．-1

  B．-2

  C．1

  D．2
  组卷：386引用：4难度：0.5

  解析

• 4．从1、2、3、4、5中任选3个不同数字组成一个三位数，则该三位数能被3整除的概率为（　　）

  A． 1 10

  B． 1 5

  C． 3 10

  D． 2 5
  组卷：220引用：7难度：0.7

  解析

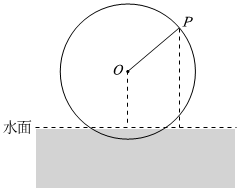• 5．半径为2m的水轮如图所示，水轮的圆心O距离水面

  3

  m.已知水轮按逆时针方向每分钟转4圈，水轮上的点P到水面的距离y（单位：m）与时间x（单位：s）满足关系式

  y

  =

  A

  sin

  （

  ωx

  -

  π

  3

  ）

  +

  k

  ．从点P离开水面开始计时，则点P到达最高点所需最短时间为（　　）

  A． 85 4 s

  B． 25 4 s

  C． 35 4 s

  D．10s
  组卷：149引用：3难度：0.6

  解析

• 6．上、下底面均为等边三角形的三棱台的所有顶点都在同一球面上，若三棱台的高为

  3

  ，上、下底面边长分别为

  3

  ，

  2

  3

  ，则该球的体积为（　　）

  A． 32 π 3

  B． 32 3 π 27

  C． 4 3 π

  D．36π
  组卷：129引用：4难度：0.6

  解析

• 7．已知椭圆C：

  x

  2

  a

  2

  +

  y

  2

  b

  2

  =

  1

  （a＞b＞0），F为其左焦点，直线y=kx（k＞0）与椭圆C交于点A，B，且AF⊥AB．若∠ABF=30°，则椭圆C的离心率为（　　）

  A． 7 3

  B． 6 3

  C． 7 6

  D． 6 6
  组卷：799引用：5难度：0.6

  解析

四、解答题（共6个小题，共70分；解答写出必要文字说明、证明过程或演算步骤）

• 21．已知双曲线

  C

  ：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  ，（a＞0，b＞0）的一条渐近线方程是x-2y=0，坐标原点到直线AB的距离为

  2

  5

  5

  ，其中A（a,0），B（0，-b）．
  （1）求双曲线C的标准方程；
  （2）过点D（2，1）直线l与双曲线C交于M，N两个不同的点，过M作x轴的垂线分别交直线AB，直线AN于点P，Q．证明：P是MQ的中点．
  组卷：133引用：2难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  a

  x

  +

  lnx

  -

  2

  （

  a

  ∈

  R

  ）

  ．
  （1）讨论f（x）的单调性；
  （2）若方程

  f

  （

  x

  ）

  =

  a

  x

  2

  +

  a

  x

  有两个不同的实数根，求a的取值范围．
  组卷：209引用：7难度：0.4

  解析