2023-2024学年陕西省西安市雁塔区高新一中博雅班九年级（上）第一次月考数学试卷

一．选择题（共8小题）

• 1．下列函数中，是二次函数的是（　　）

  A．y=2x+1

  B．y= 2 x

  C．y=x2+2

  D．y=2x
  组卷：386引用：5难度：0.8

  解析

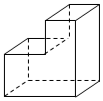• 2．从上面看如图几何体得到的平面图形是（　　）

  A．

  B．

  C．

  D．
  组卷：227引用：4难度：0.8

  解析

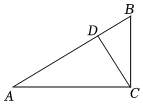• 3．如图，在Rt△ABC中，CD是斜边AB上的高，∠A≠45°，则下列比值中不等于cosB的是（　　）

  A． CD AC

  B． BD CB

  C． CD CB

  D． CB AB
  组卷：687引用：6难度：0.5

  解析

• 4．关于x的一元二次方程kx²+2x+1=0有两个实根，则实数k的取值范围是（　　）

  A．k≤1

  B．k＜1

  C．k≤1且k≠0

  D．k＜1且k≠0
  组卷：2320引用：31难度：0.9

  解析

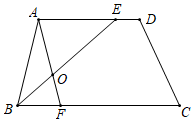• 5．如图，在四边形ABCD中，AD∥BC，点E，F分别是边AD，BC上的点，AF与BE交于点O，AE=2，BF=1，则△AOE与△BOF的面积之比为（　　）

  A． 1 2

  B． 1 4

  C．2

  D．4
  组卷：597引用：5难度：0.8

  解析

• 6．已知四边形ABCD是平行四边形，下列结论：
  ①当AB=BC时，它是菱形；
  ②当AC⊥BD时，它是菱形；
  ③当∠ABC=90°时，它是矩形；
  ④当AC=BD时，它是正方形．
  四个结论中正确的是（　　）

  A．仅①正确

  B．①②正确

  C．①②③正确

  D．①②③④都正确
  组卷：286引用：4难度：0.7

  解析

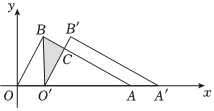• 7．如图，在平面直角坐标系中，点A的坐标为（4，0），B为第一象限内一点，且OB⊥AB，OB=2．将△OAB沿x轴向右平移得到△O′A′B′，O'B'与AB交于点C，若OO′=1，则△BCO'的面积为（　　）

  A． 3 8

  B． 3 4

  C． 3 3 8

  D． 3 3 4
  组卷：501引用：3难度：0.5

  解析

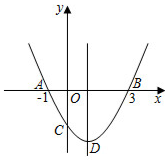• 8．抛物线y=ax²+bx+c（a≠0）交x轴于A（-1，0），B（3，0），交y轴的负半轴于C，顶点为D．下列结论：①abc＜0；②2a+b=0；③2a+c＞0；④当m≠1时，a+b＜am²+bm,⑤若E（x₁，y₁），F（x₂，y₂），G（x₃，y₃）为抛物线上三点，且-1＜x₁＜x₂＜1，x₃＞3，则y₂＜y₁＜y₃；⑥当△ABD是等腰直角三角形时，则a=

  1

  2

  ；其中正确的有（　　）个．

  A．5

  B．4

  C．3

  D．2
  组卷：102引用：2难度：0.6

  解析

三．解答题（共13小题）

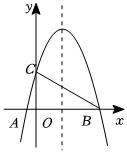• 25．如图，抛物线y=-x²+bx+c（a,b,c是常数，且a≠0）与x轴交于A，B两点，与y轴交于点C（0，3），对称轴为直线x=1．
  （1）求抛物线的函数表达式；
  （2）点F在抛物线的对称轴上，若线段FB绕点F逆时针旋转90°后，点B的对应点B'恰好也落在此抛物线上，请求出点F的坐标．
  组卷：224引用：2难度：0.3

  解析

• 26．问题背景：
  一次数学综合实践活动课上，小慧发现并证明了关于三角形角平分线的一个结论．如图1，已知AD是△ABC的角平分线，可证

  AB

  AC

  =

  BD

  CD

  小慧的证明思路是：如图2，过点C作CE∥AB，交AD的延长线于点E，构造相似三角形来证明．
  
  （1）尝试证明：请参照小慧提供的思路，利用图2证明

  AB

  AC

  =

  BD

  CD

  ；
  （2）基础训练：如图3，在Rt△ABC中，∠BAC=90°，D是边BC上一点．连接AD，将△ACD沿AD所在直线折叠，点C恰好落在边AB上的E点处．若AC=1，AB=2，求DE的长；
  （3）拓展升华：如图4，△ABC中，AB=6，AC=4，AD为∠BAC的角平分线，AD的中垂线EF交BC延长线于F，当BD=3时，求AF的长．
  组卷：656引用：5难度：0.1

  解析