2022-2023学年甘肃省庆阳二中高二(下)第一次月考数学试卷
发布:2024/6/22 8:0:10
一、选择题(每小题5分,共8小题40分)
-
1.已知{
,a,b}是空间的一个基底,{c+a,b-a,b}是空间的另一个基底,一向量c在基底{p,a,b}下的坐标为(4,2,3),则向量c在基底{p+a,b-a,b}下的坐标是( )c组卷:423引用:14难度:0.9 -
2.函数f(x)=2x-5lnx-4的单调递增区间是( )
组卷:281引用:8难度:0.7 -
3.定义满足方程f'(x)+f(x)=1的实数解x0叫做f(x)函数的“自足点”,则下列函数存在“自足点”的是( )
组卷:117引用:4难度:0.7 -
4.设函数f(x)=x2+x,则
limΔx→0=( )f(1+△x)-f(1)△x组卷:1455引用:6难度:0.9 -
5.设a=ln3,
,b=3ln2,则a、b、c的大小关系是( )c=2ln3组卷:516引用:9难度:0.4 -
6.已知空间向量
,且a=(-1,2,1),b=(3,x,-3)∥a,则x=( )b组卷:244引用:4难度:0.7 -
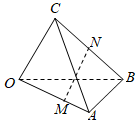 7.如图,空间四边形OABC中,=OA,a=OB,b=OC,且OM=2MA,BN=NC,则c等于( )MN组卷:2762引用:44难度:0.8
7.如图,空间四边形OABC中,=OA,a=OB,b=OC,且OM=2MA,BN=NC,则c等于( )MN组卷:2762引用:44难度:0.8
四、解答题(第17题10分,其余每小题10分,共6小题70分)
-
21.已知函数
,(a∈R).f(x)=lnx-ax-12x3
(1)若曲线y=f(x)在点(1,f(1))处的切线经过点,求a的值;(3,92)
(2)当x>0时,f(x)<0恒成立,求a的取值范围.组卷:88引用:3难度:0.5 -
22.已知函数f(x)=exln(1+x).
(Ⅰ)求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)设g(x)=f′(x),讨论函数g(x)在[0,+∞)上的单调性;
(Ⅲ)证明:对任意的s,t∈(0,+∞),有f(s+t)>f(s)+f(t).组卷:5842引用:17难度:0.4


