2023-2024学年山东省德州市庆云县渤海中学八年级（上）第一次调研数学试卷
发布：2024/9/26 13:0:2
一、选择题（本题共12小题，每小题4分，共48分）．
-
1．下列各组数可能是一个三角形的边长的是（ ）
组卷：284引用：29难度：0.6 -
2．下列图形不具有稳定性的是（ ）
组卷：544引用：48难度：0.9 -
3．如图，把一副含30°角和45°角的直角三角板拼在一起，那么图中∠ADE是（ ）组卷：184引用：8难度：0.9 -
4．一个正多边形，它的每一个外角都等于40°，则该正多边形是（ ）
组卷：1358引用：19难度：0.9 -
5．如图，△ABC≌△BAD，点A和点B，点C和点D是对应点，如果AB=6cm,BD=5cm,AD=4cm,那么AC的长是（ ）组卷：367引用：22难度：0.9 -
6．如图所示，a、b、c分别表示△ABC的三边长，则下面与△ABC一定全等的三角形是（ ）组卷：222引用：22难度：0.6 -
7．如图，△ABC和△DEF中，AB=DE、∠B=∠DEF，添加下列哪一个条件无法证明△ABC≌△DEF（ ）组卷：4399引用：131难度：0.7 -
8．如图，AD是△ABC的中线，CE是△ACD的中线，DF是△CDE的中线，如果△DEF的面积是2，那么△ABC的面积为（ ）组卷：1734引用：13难度：0.9
三、解答题（本题共7题，共78分）．
-
24．（1）【初步探索】如图①，在四边形ABCD中，BA=BC，∠A=∠C=90°．E、F分别是AD、CD上的点．且EF=AE+CF．探究图中∠CBF、∠EBF、∠ABE之间的数量关系．小王同学探究此问题的方法：延长EA到点G，使AG=CF．连接BG．先证明△BCF≌△BAG，再证△BEF≌△BEG，可得出结论．他的结论应是 ．
（2）【灵活运用】如图②，在四边形ABCD中，BA=BC，∠A+∠C=180°，E、F分别是AD、CD上的点，且EF=AE+CF，上述结论是否仍然成立？请说明理由．
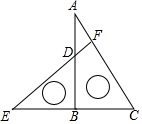
（3）【延伸拓展】如图③，在四边形ABCD中，∠BAD+∠BCD=180°，BA=BC．若点E在DA的延长线上，点F在DC的延长线上，仍然满足EF=AE+CF，请写出∠EBF与∠ABC的数量关系，并给出证明过程．
组卷：249引用：4难度：0.5 -
25．（1）阅读理解：如图1，在△ABC中，若AB=3，AC=5．求BC边上的中线AD的取值范围，小聪同学是这样思考的：延长AD至E，使DE=AD，连接BE．利用全等将边AC转化到BE，在△BAE中利用三角形三边关系即可求出中线AD的取值范围，在这个过程中小聪同学证三角形全等用到的判定方法是 ，中线AD的取值范围是 ；
（2）问题解决：如图2，在△ABC中，点D是BC的中点，DM⊥DN．DM交AB于点M，DN交AC于点N．求证：BM+CN＞MN；
（3）问题拓展：如图3，在△ABC中，点D是BC的中点，分别以AB，AC为直角边向△ABC外作Rt△ABM和Rt△ACN，其中∠BAM=∠NAC=90°，AB=AM，AC=AN，连接MN，请你探索AD与MN的数量与位置关系，并直接写出AD与MN的关系．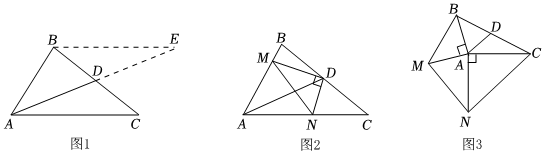
组卷：358引用：20难度：0.1
