2022-2023学年山东省济南市莱芜一中高二(下)期中数学试卷
发布:2024/6/1 8:0:9
一、选择题:本大题共8小题:每小题5分,共40分,在每小题给出的四个选项中,只有一项是量符合题目要求的。
-
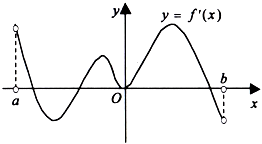 1.函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )组卷:125引用:10难度:0.8
1.函数f(x)的定义域为开区间(a,b),导函数f′(x)在(a,b)内的图象如图所示,则函数f(x)在开区间(a,b)内有极小值点( )组卷:125引用:10难度:0.8 -
2.设集合A⊆B,且P(A)=0.2,P(B)=0.7,则下列说法正确的是( )
组卷:792引用:7难度:0.7 -
3.下列有关排列数、组合数的计算,正确的是( )
组卷:269引用:2难度:0.8 -
4.设x是一个离散型随机变量,其分布列如下,则q等于( )
X -1 0 1 P 131-2q 3q2-q+ 13组卷:130引用:1难度:0.7 -
5.为有效阻断新冠肺炎疫情传播徐径,构筑好免疫屏障,从2022年1月13日开始,某市启动新冠病毒疫苗加强针接种工作,凡符合接种第三针条件的市民,要求尽快接种.该市有3个疫苗接种定点医院,现有8名志愿者将被派往这3个医院协助新冠疫苗接种工作,每个医院至少2名至多4名志愿者,则不同的安排方法共有( )
组卷:447引用:5难度:0.7 -
6.已知定义在区间
上的奇函数y=f(x),对于任意的(-π2,π2)满足f'(x)cosx+f(x)sinx>0(其中f'(x)是f(x)的导函数),则下列不等式中成立的是( )x∈[0,π2)组卷:241引用:3难度:0.4 -
7.随机变量X的分布列如下所示.则D(bX)的最大值为( )
X 1 2 3 P a 2b a 组卷:165引用:7难度:0.6
四、解答题:本大题共6小题,共70分。其中17题10分,其余题目12分,解答应写出文字说明证明过程或演算步骤。
-
21.已知函数f(x)=
x2+2alnx-2x(a∈R).12
(1)若函数f(x)在区间(1,2)上不单调,求a的取值范围;
(2)令F(x)=f(x)-ax,当a>0时,求F(x)在区间[1,2]上的最大值.组卷:62引用:1难度:0.6 -
22.已知函数f(x)=ex-lnx.
(1)求证:f(x)>2;
(2)若函数g(x)=f(x)-ax2-仅有两个零点,求实数a的取值范围.e+12组卷:54引用:1难度:0.5


